Year 8 Transformations Worksheets
Combining Transformations
Describing Single Transformations
Describing Enlargements (A)
Describing Enlargements (B)
Describing Rotations and Reflections
Enlargement (A)
Enlargement (B)
Enlargements on Axes
Enlargements Using Column Vectors
Lines of Symmetry
Make it Symmetrical
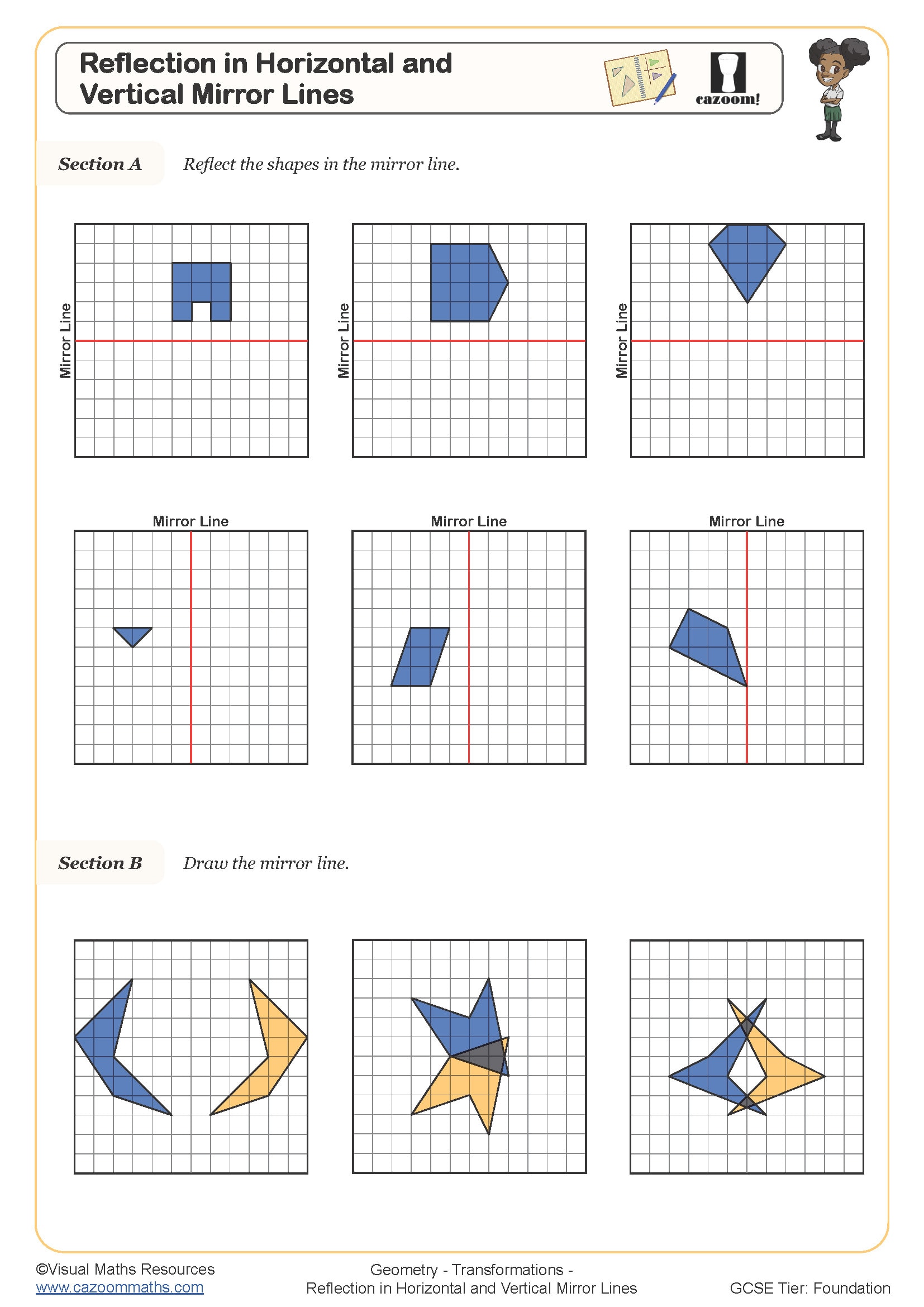
Refelction in Horizontal and Vertical Mirror Lines
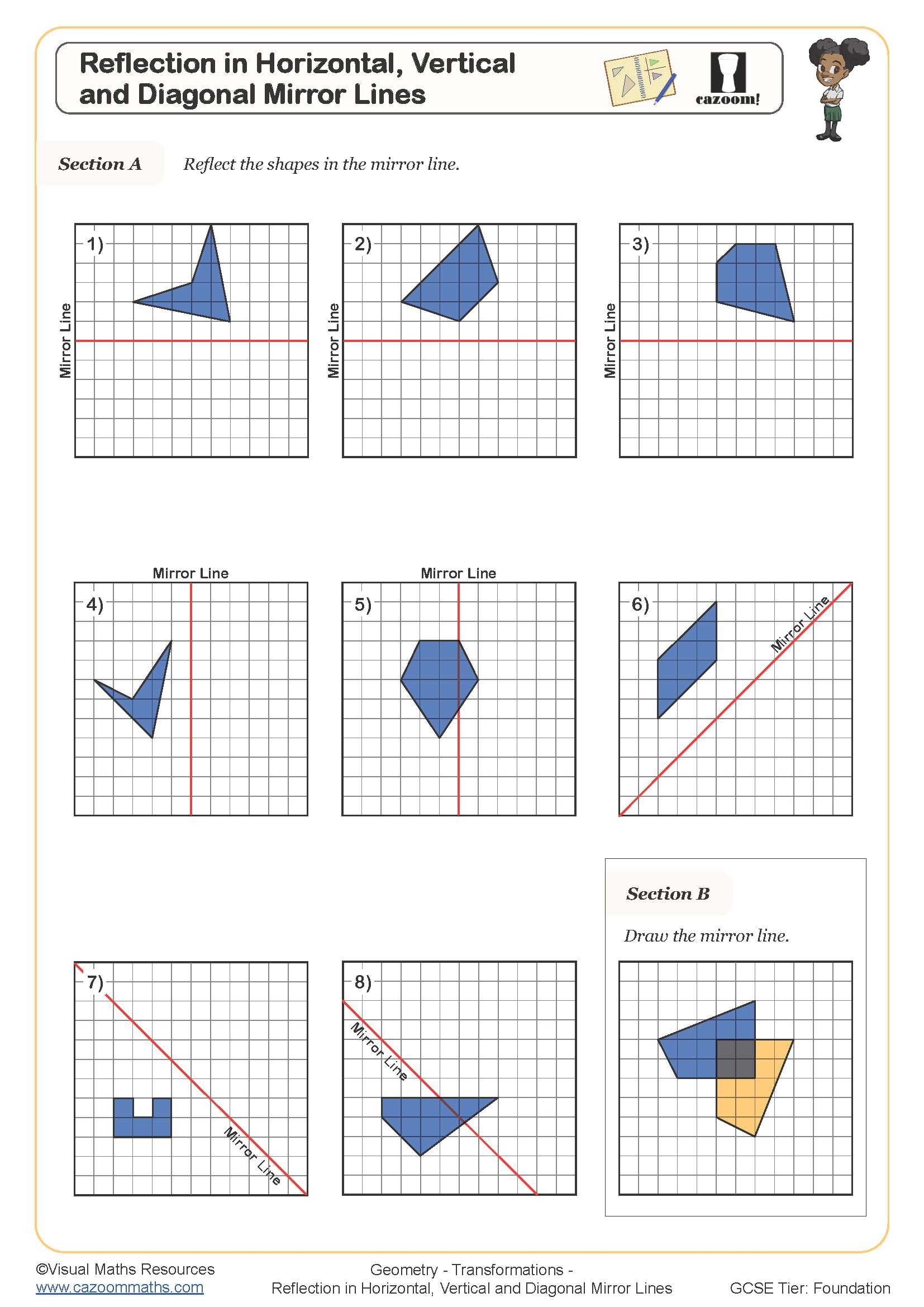
Reflection in Horizontal, Vertical and Diagonal Mirror Lines
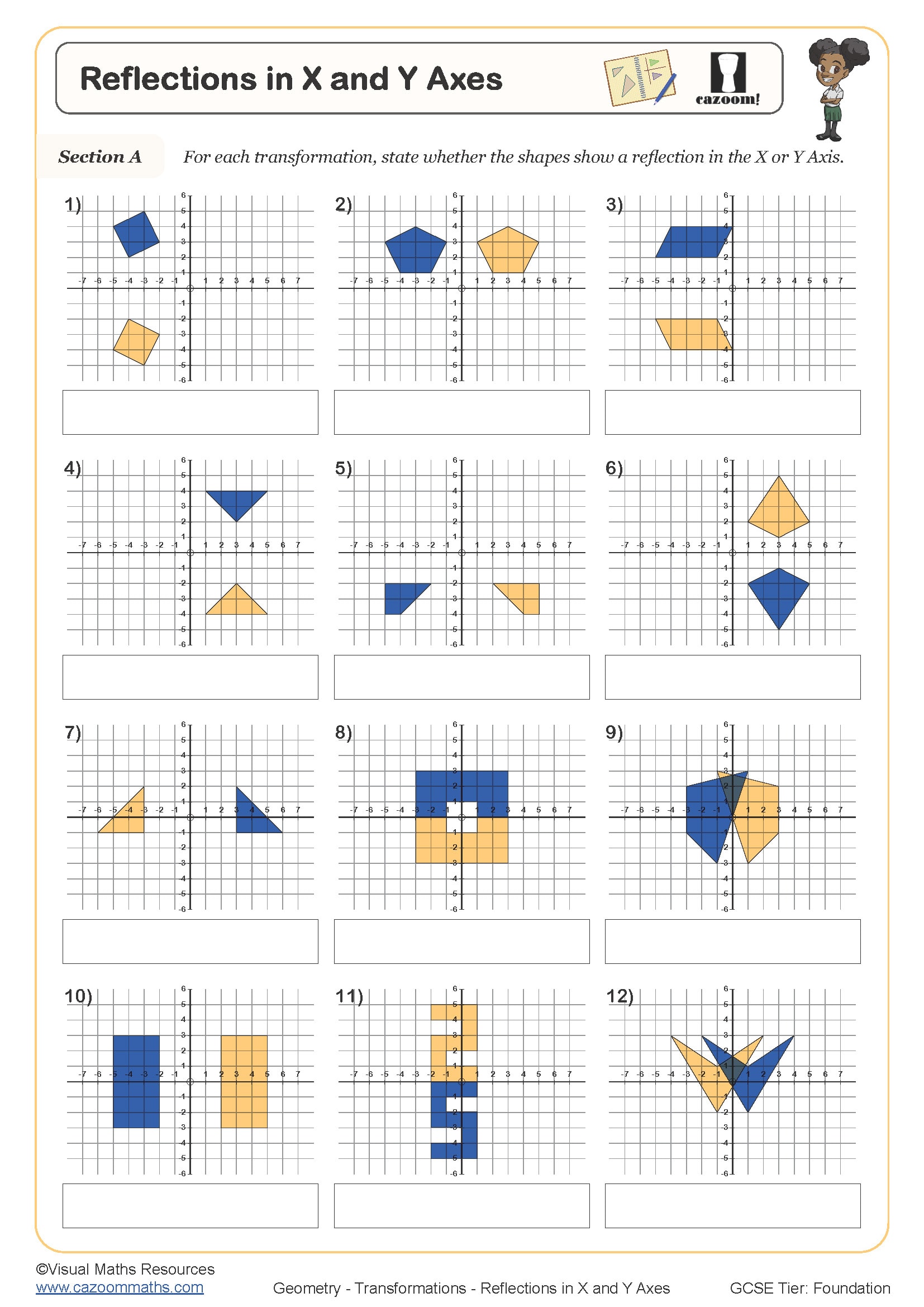
Reflections in X and Y Axes
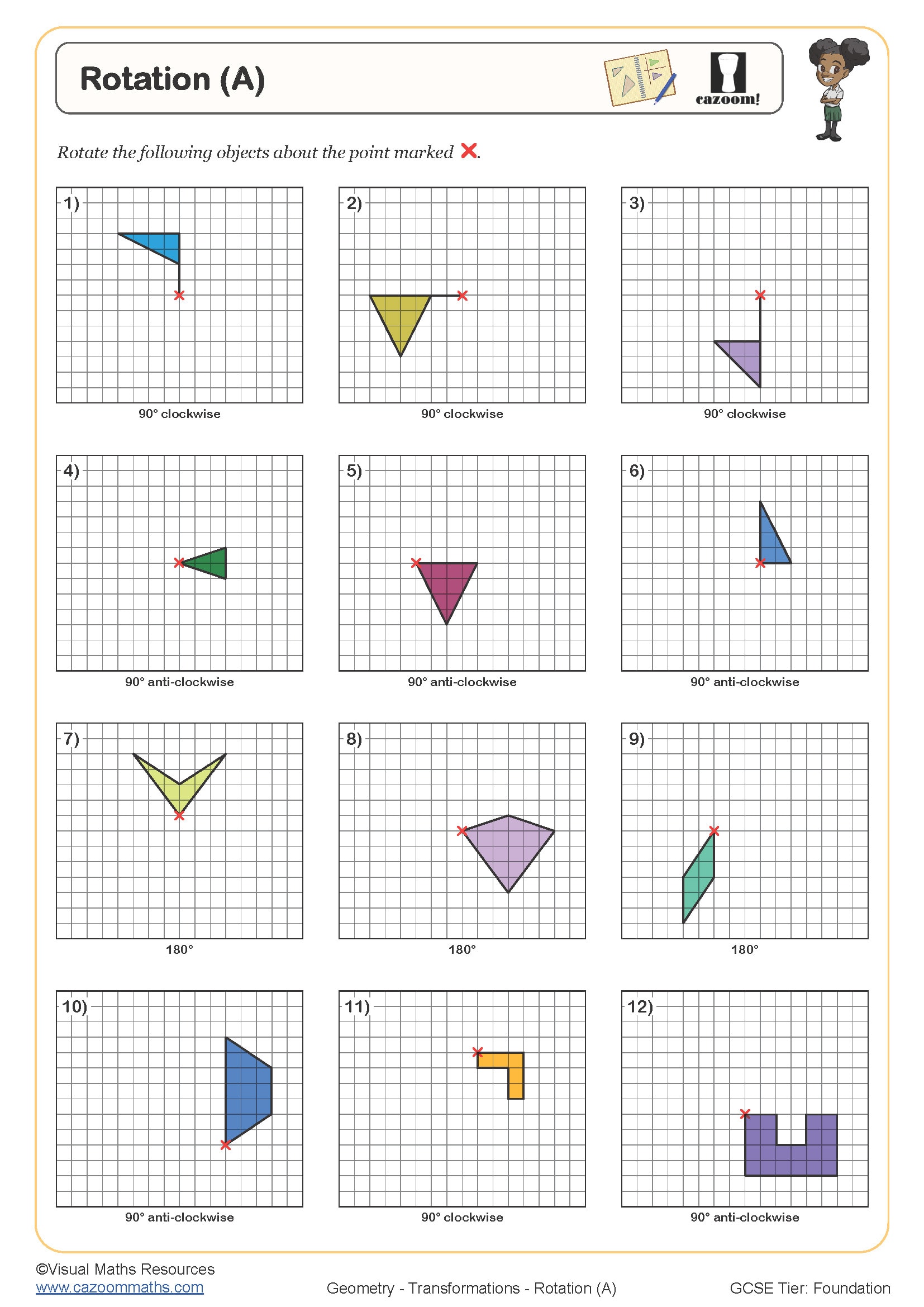
Rotation (A)
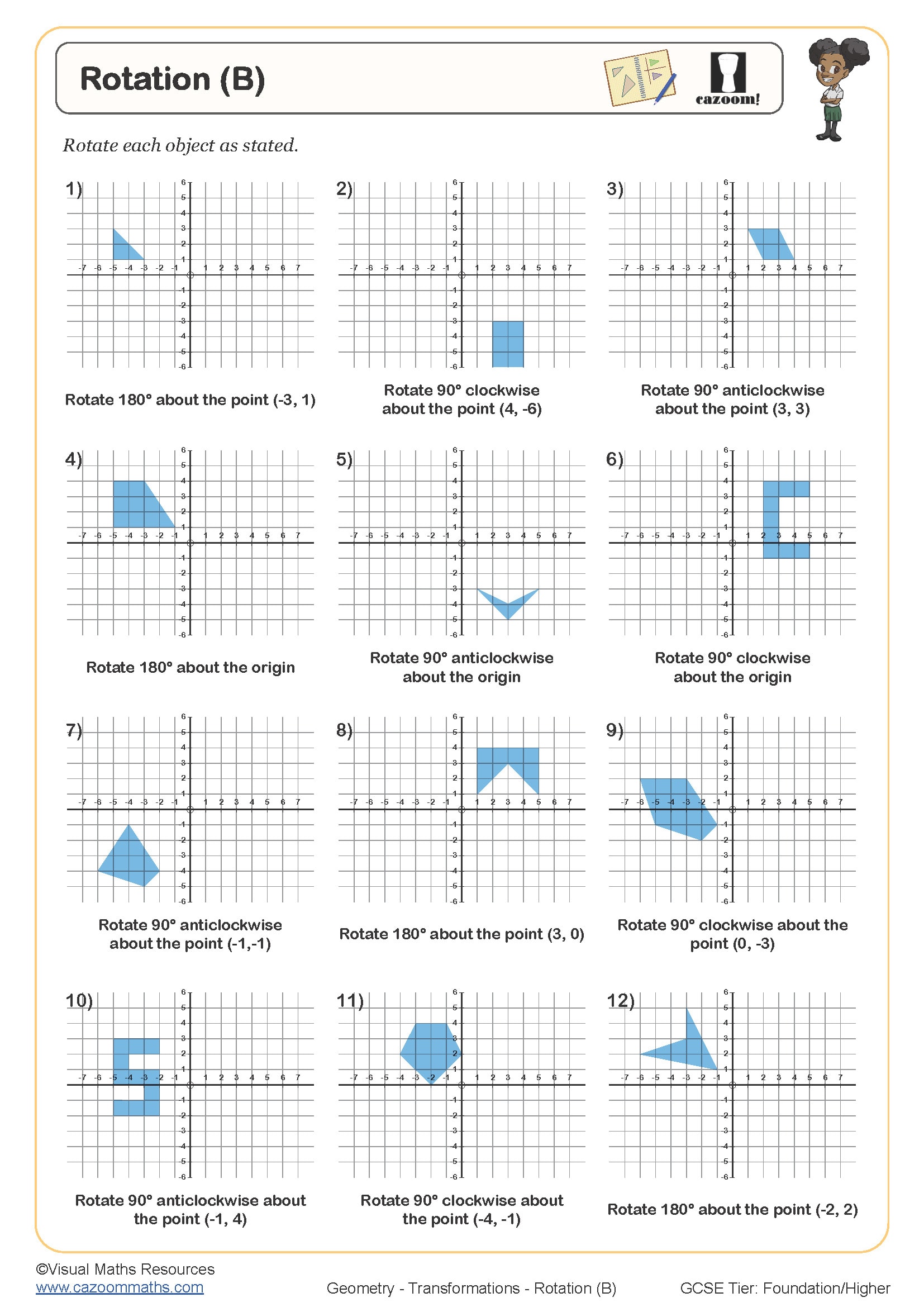
Rotation (B)
Rotation (C)
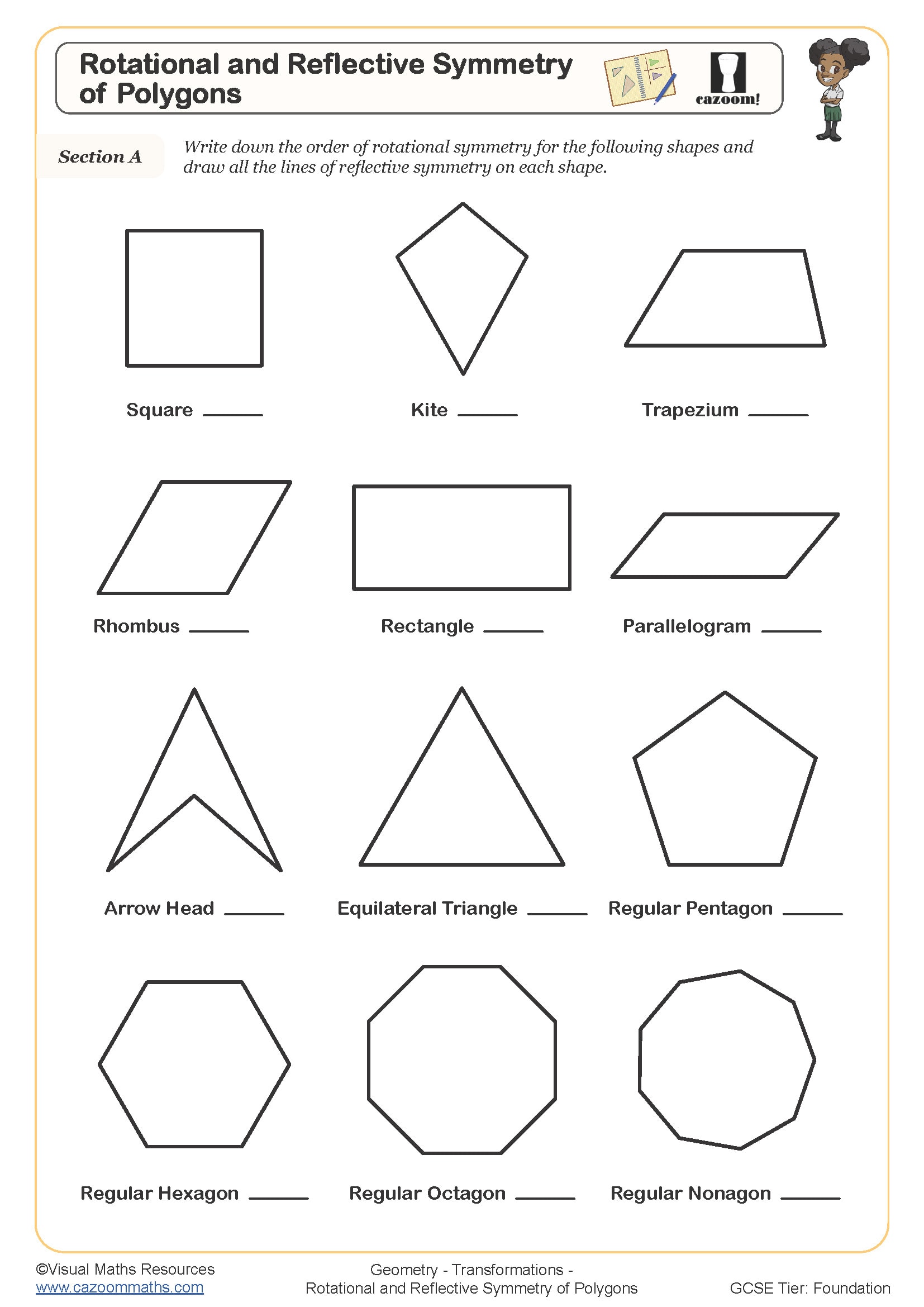
Rotational and Refelctive Symmetry of Polygons
Scale Factors and Centres of Enlargement (A)
Scale Factors and Centres of Enlargement (B)
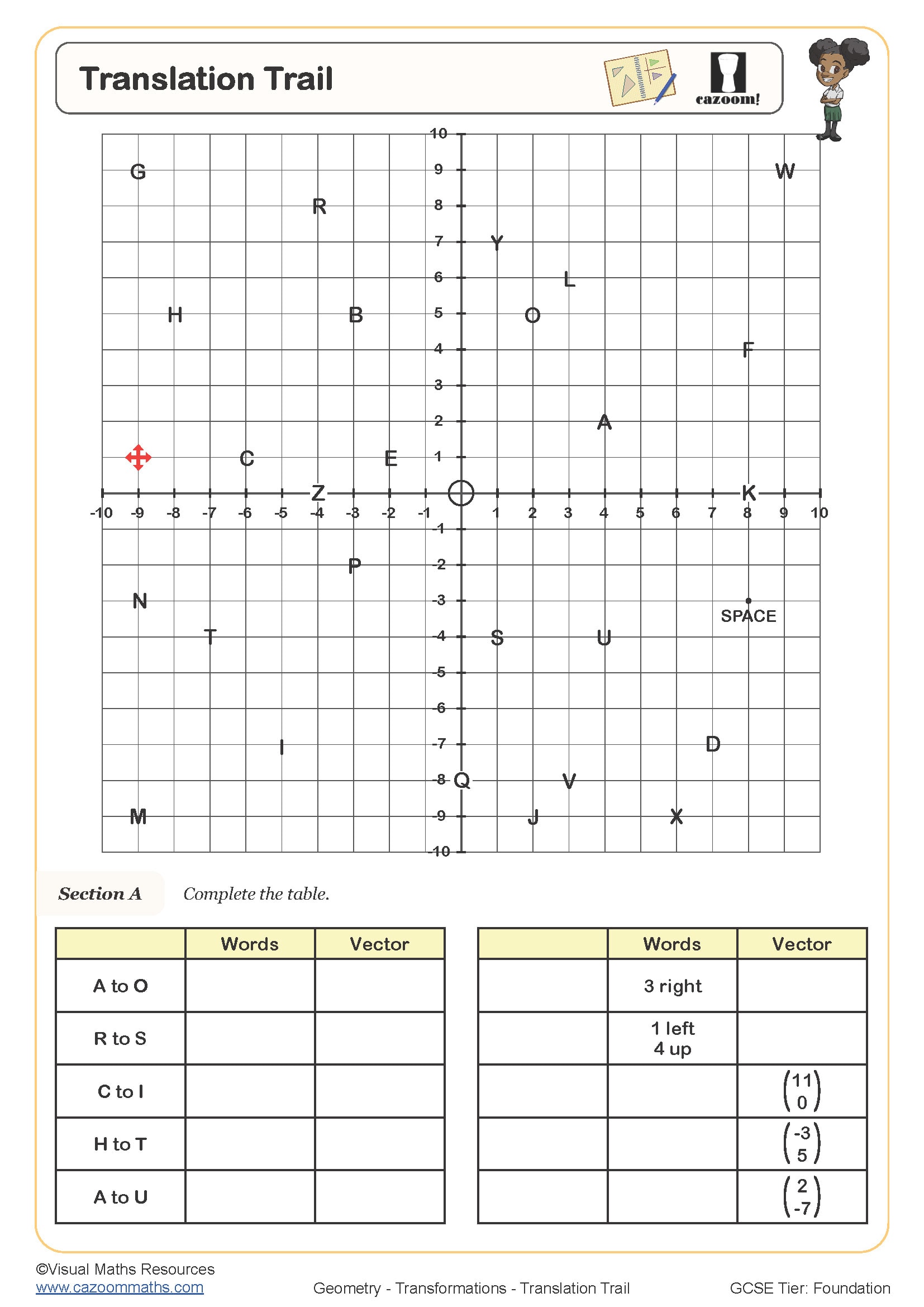
Translation Trail
Translations - from Column Vectors
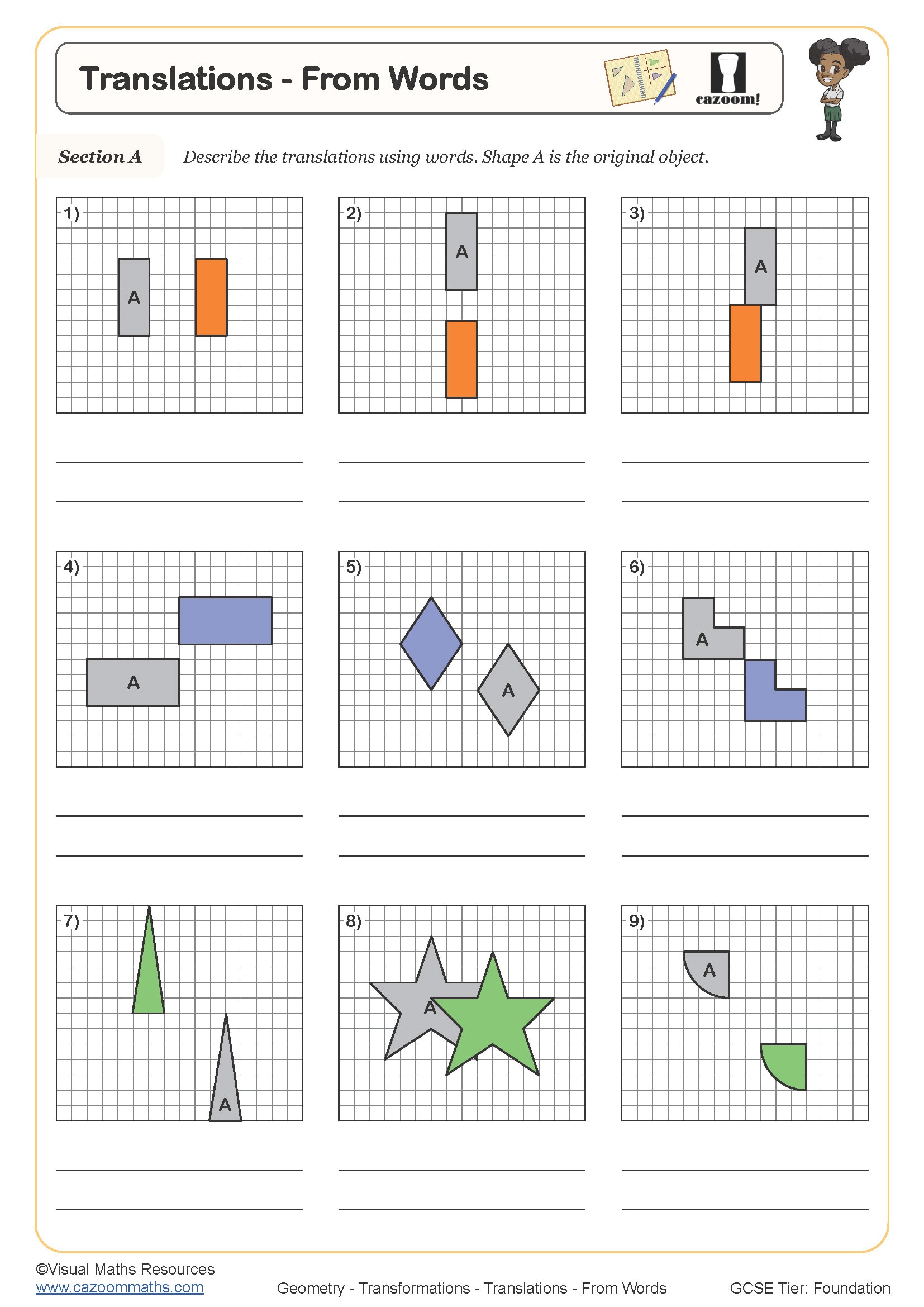
Translations - from Words
How Our Ready-to-use Transformations Activities Strengthen Geometrical Understanding in Year 8
Regular transformations practice develops crucial spatial reasoning skills that underpin advanced geometry and algebraic concepts throughout secondary education. Students create mental images of shape movements before performing them, which helps them predict outcomes and check their accuracy. Students need to use coordinate grids to find exact locations while performing their work and to measure exact angles and distances. The method establishes a systematic link between visual comprehension and formal mathematical notation, enabling students to understand vectors, matrices, and complex numbers. Students learn adaptable problem-solving techniques through mental manipulation after mastering tracing paper methods, which helps them maintain accuracy in their work.
Specific learning benefits include:
• Master coordinate notation for precise positioning
• Strengthens mental rotation abilities
• Develops systematic checking methods
• Builds fluency with negative coordinates
• Establishes foundations for vector work
• Improves spatial reasoning skills
Year 8 Transformations Content Topics: From Basic Movements to Combined Transformations
Our carefully sequenced worksheets progress from concrete visual examples through pictorial representations to abstract mathematical descriptions, ensuring every student can access the content at their level. Each resource includes worked solutions showing complete methods and reasoning, allowing independent study and self-correction. Students begin with single transformations before tackling combinations, developing methodical approaches to complex problems.
The worksheets in this collection include:
• Reflections in Horizontal and Vertical Lines — identifying mirror lines parallel to axes
• Reflections in Diagonal Lines — working with y=x and y=-x as mirror lines
• Rotations About the Origin — practising quarter, half and three-quarter turns
• Rotations About Any Point — using tracing paper for accuracy
• Translations Using Column Vectors — introducing vector notation systematically
• Enlargements From the Origin — applying positive integer scale factors
• Enlargements From Any Centre — finding centres and calculating distances
• Describing Single Transformations — using correct mathematical terminology throughout
• Combining Two Transformations — understanding order effects on final positions
Get Students Excited About Maths With Our Year 8 Transformations Worksheets
Teachers select these resources for their immediate usability and thoughtful differentiation across ability ranges. The worksheets contain multiple entry points which support various learning needs while avoiding the need for distinct materials for different student groups. The use of clear coordinate grids with well-spaced shapes helps students avoid transcription errors, which enables them to concentrate on transformation concepts instead of dealing with difficult-to-read diagrams. The use of a standard format in worksheets helps students develop routine skills, which shortens the time needed for instruction. Answer sheets highlight common misconceptions and provide marking shortcuts through colour-coding and clear labelling. The worksheets have a functional design that helps teachers save time for preparation and assessment while covering all curriculum content, making them useful for classroom activities, homework assignments, and revision work.
Transformations Skills Connect Mathematics to Everyday Applications
Understanding transformations unlocks numerous practical applications, ranging from digital design to engineering solutions.
Students apply transformation knowledge when:
• Programming computer animations and game graphics
• Understanding architectural plans and technical drawings
• Creating tessellating patterns in art projects
• Analysing symmetry in nature and crystallography
• Designing logos with rotational symmetry
• Planning efficient packaging and material cutting
• Interpreting maps and navigation systems
• Developing spatial awareness for sports positioning