Year 9 Pythagoras Worksheets
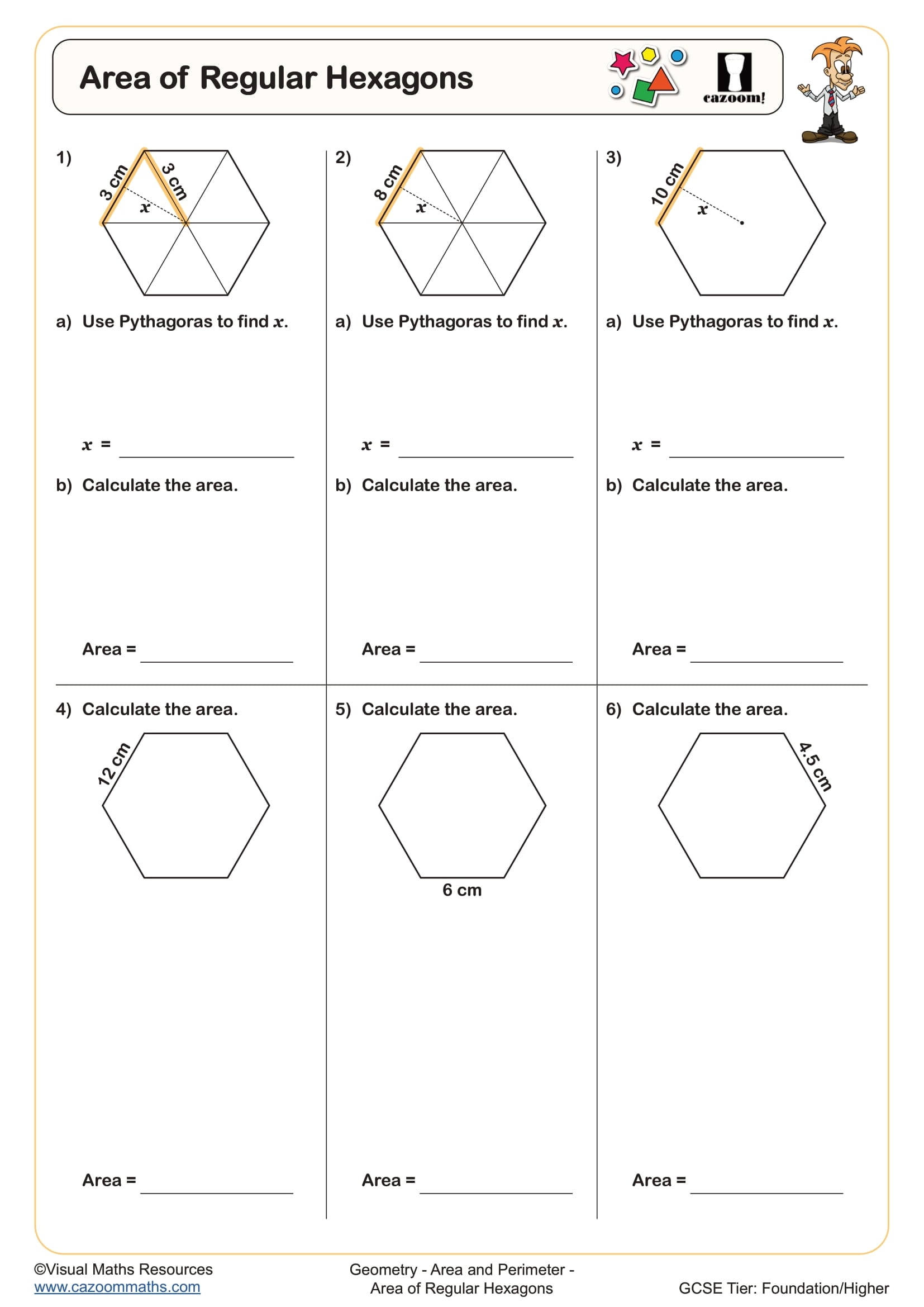
Area of Regular Hexagons
Identifying Right Angled Triangles

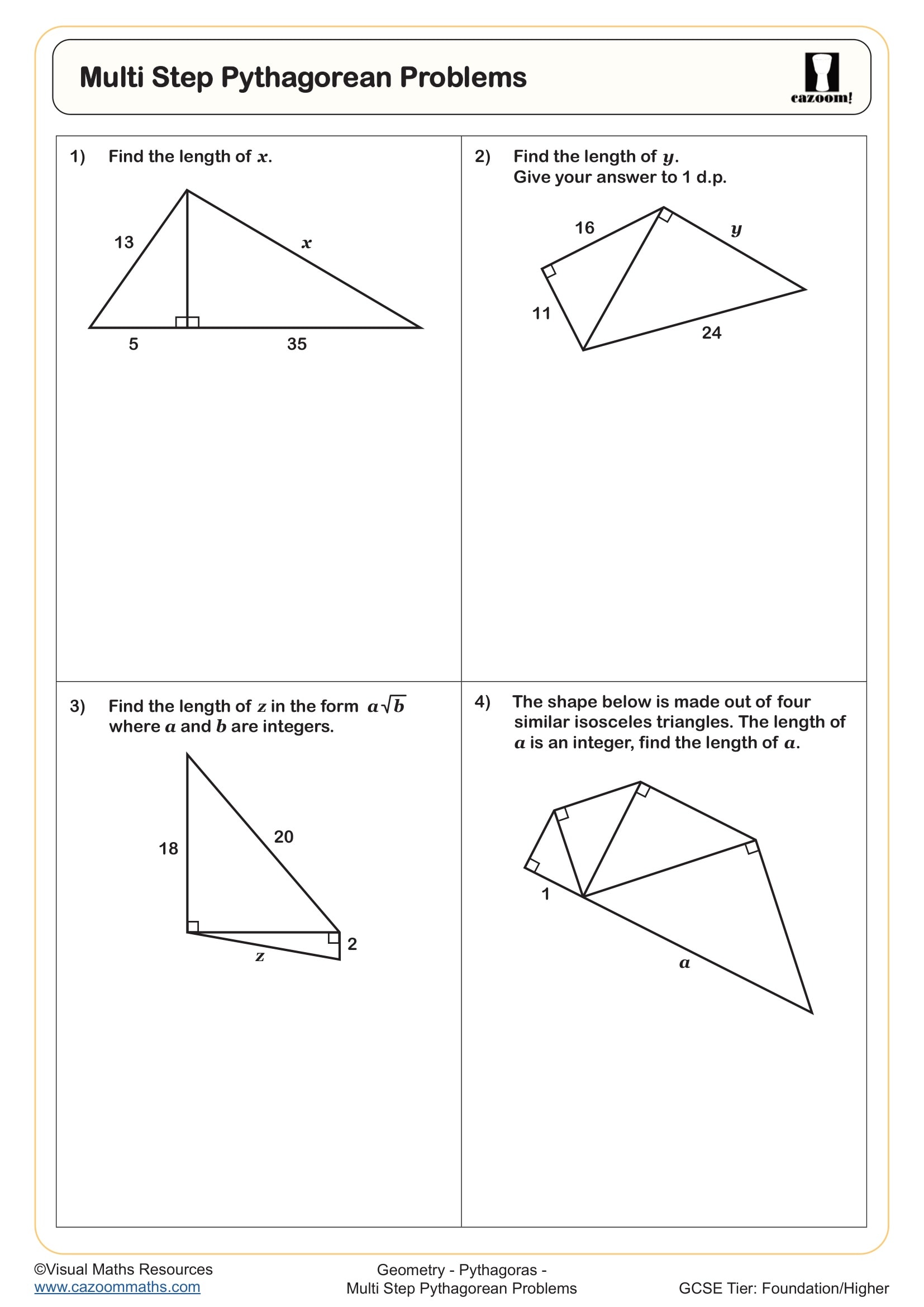
Multi Step Pythagorean Problems
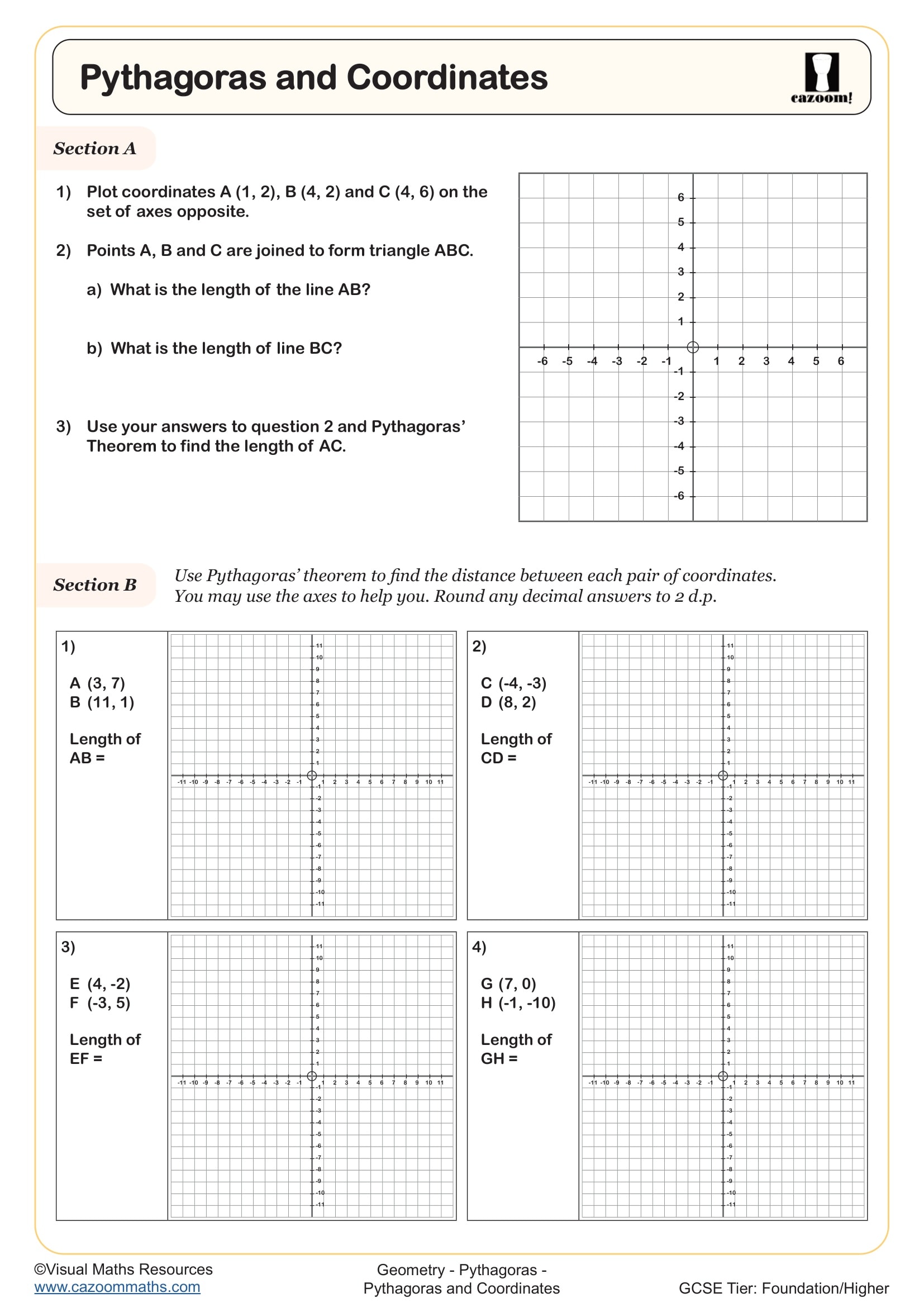
Pythagoras and Coordinates
Pythagoras Word Problems

Pythagoras Word Problems (With Clues)

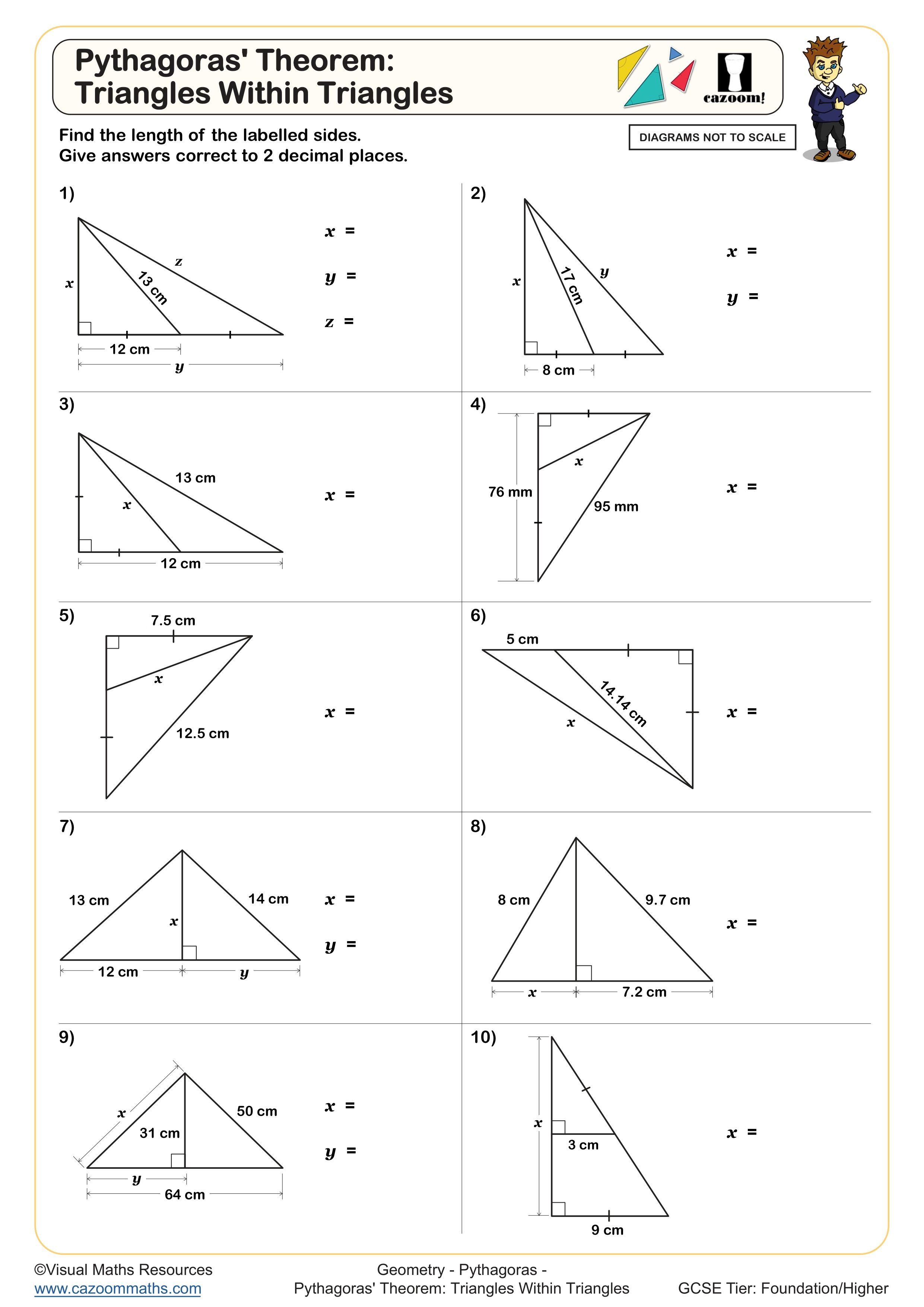
Pythagoras' Theorem: Triangles Within Triangles
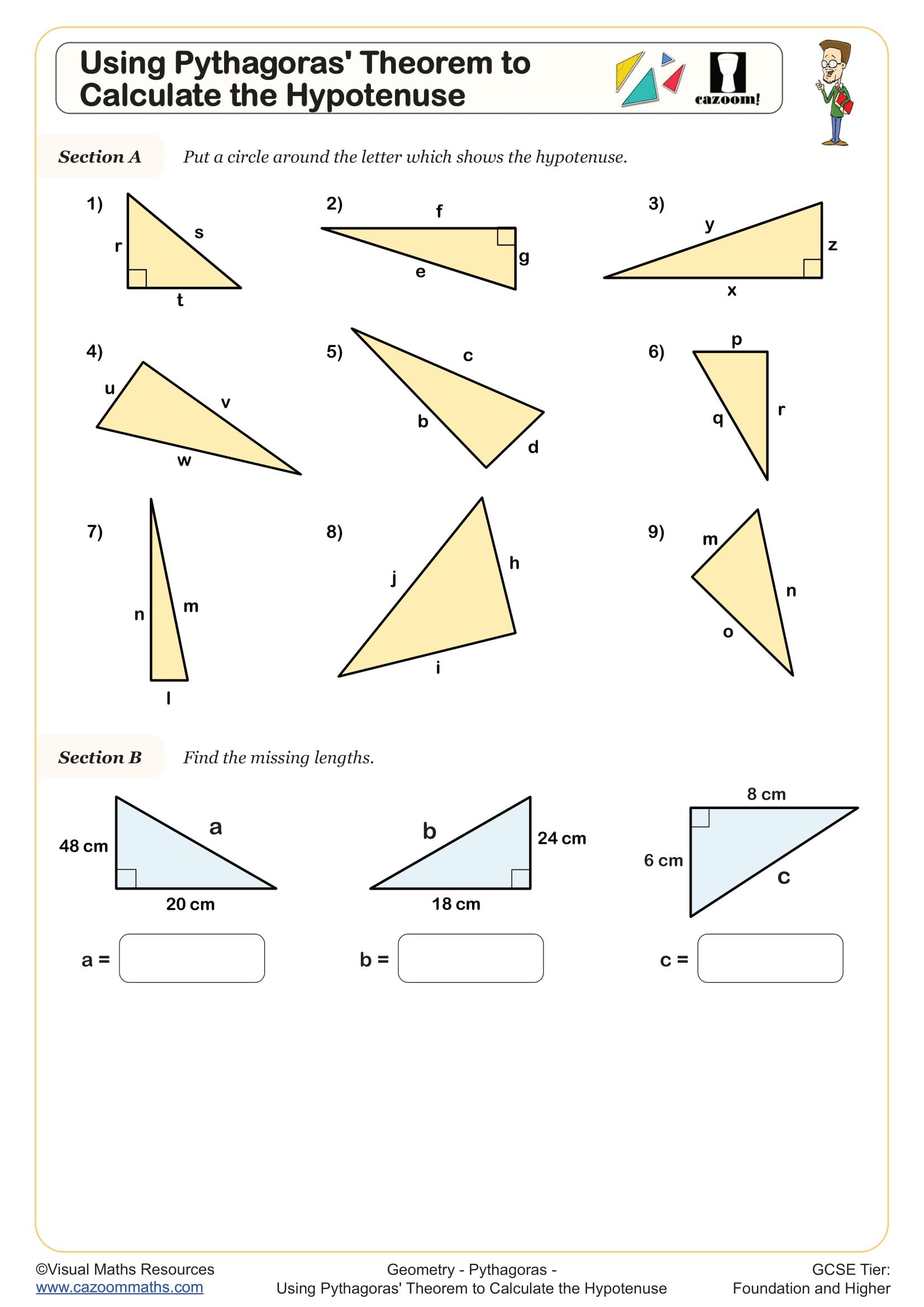
Using Pythagoras Theorem to Calculate the Hypotenuse
Using Pythagoras' Theorem to Calculate Missing Lengths in Right Angled Triangles

Raise Maths Scores With Our Printable PDF Year 9 Pythagoras Worksheets
Understanding Pythagoras' theorem gives your secondary school students the tools to solve geometric problems that go well beyond triangle calculations. Students moving from Year 8 shape work to algebra and geometry find strong links between the two subjects through repeated square root operations and rearranging equations. Moving from simple length calculations to more complicated 3D situations helps people learn how to visualise space, which is important for engineering, architecture, and science. Regularly working on different types of problems makes students more resilient in maths because they have to do more complicated calculations. This methodical exposure prevents gaps in understanding that could make it hard to understand trigonometry at the GCSE level.
Specific learning benefits include:
• Strengthens algebraic manipulation through square roots
• Develops spatial visualisation in three dimensions
• Connects coordinate geometry with distance formulae
• Builds systematic problem-solving approaches
• Enhances calculator accuracy and efficiency
• Establishes foundations for trigonometric ratios
• Improves mathematical communication skills
Worksheet Topics at a Glance: Pythagoras' Theorem, Right Angled Triangles, and More
These worksheets guide students from concrete visual representations to pictorial diagrams to abstract formula application, with fully worked solutions showing how to use all of the steps in a mathematical reasoning process. Teachers have the ability to select the best starting points for each student while still covering the whole curriculum. The resources include simple identification tasks to hard real-world problems, which makes it easy to teach in different ways in the classroom.
The worksheets in this collection include:
• 3D Pythagoras (A) — extends the theorem application into three-dimensional space calculations.
• Area of Regular Hexagons — combines Pythagorean relationships with polygon area formulae.
• Identifying Right Angled Triangles — develops recognition skills using the converse theorem.
• Multi-Step Pythagorean Problems — challenge learners with compound geometric scenarios.
• Pythagoras and Coordinates — links the theorem to the distance between coordinate points.
• Pythagoras Word Problems — applies mathematical reasoning to contextualised situations.
• Pythagoras Word Problems (With Clues) — provides scaffolded support for problem interpretation.
• Using Pythagoras' Theorem to Calculate the Hypotenuse — focuses on finding the longest side lengths.
• Using Pythagoras' Theorem to Calculate Missing Lengths in Right-Angled Triangles — practice finding any unknown side systematically.
Why Schools Choose Cazoom Maths Year 9 Geometry Resources for Easy Learning
Secondary mathematics departments choose Cazoom Maths resources for their immediate usability and time-saving design elements. During class lessons, homework assignments, or revision sessions, KS3 students can work independently because of the clear layouts that gradually increase in difficulty. All of our activities include separate answer sheets that offer exemplar solutions for peer assessment tasks while reducing the workload associated with marking. Diagrams complement algebraic methods throughout, and visual representations accommodate a variety of learning preferences. For advanced learners, extension challenges keep them interested without requiring the creation of additional resources. Worksheets for Cazoom Maths easily fit into current work plans, promoting standardised departmental methodologies.
Where Students Apply Pythagorean Thinking Outside Mathematics Lessons
Understanding right-angled triangle relationships empowers students to solve measurement and distance problems encountered across numerous fields. These fundamental geometric principles underpin professional practices and everyday decision-making. For example-
• Navigation apps calculate the shortest routes between destinations.
• Video game physics engines determining projectile paths
• Construction teams are measuring diagonal support beams.
• Smartphone screens detecting touch position coordinates
• Drone pilots plan flight paths around obstacles.
• Interior designers optimising room layouts and furniture placement
• Sound engineers positioning speakers for acoustic coverage
• Archaeological teams mapping excavation site dimensions