KS3 Algebra Tiles Worksheets
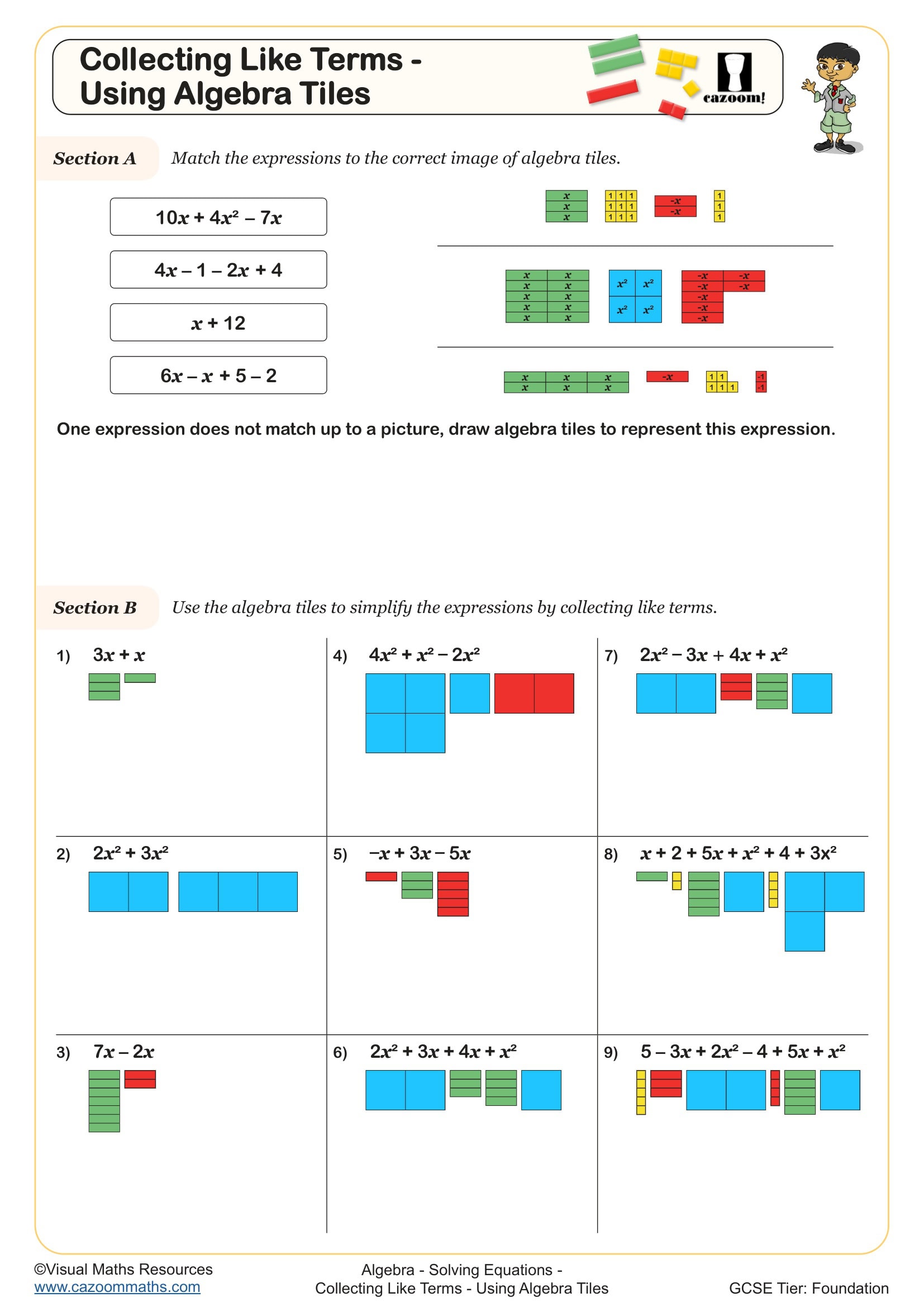
Collecting Like Terms - Using Algebra Tiles
Directed Number - Addition Using Directed Counters

Directed Number - Multiplication Using Directed Number Counters

Directed Number - Subtraction Using Directed Counters

Expanding Brackets and Simplifying - Using Algebra Tiles

Expanding Double Brackets (A) Using the Grid Method

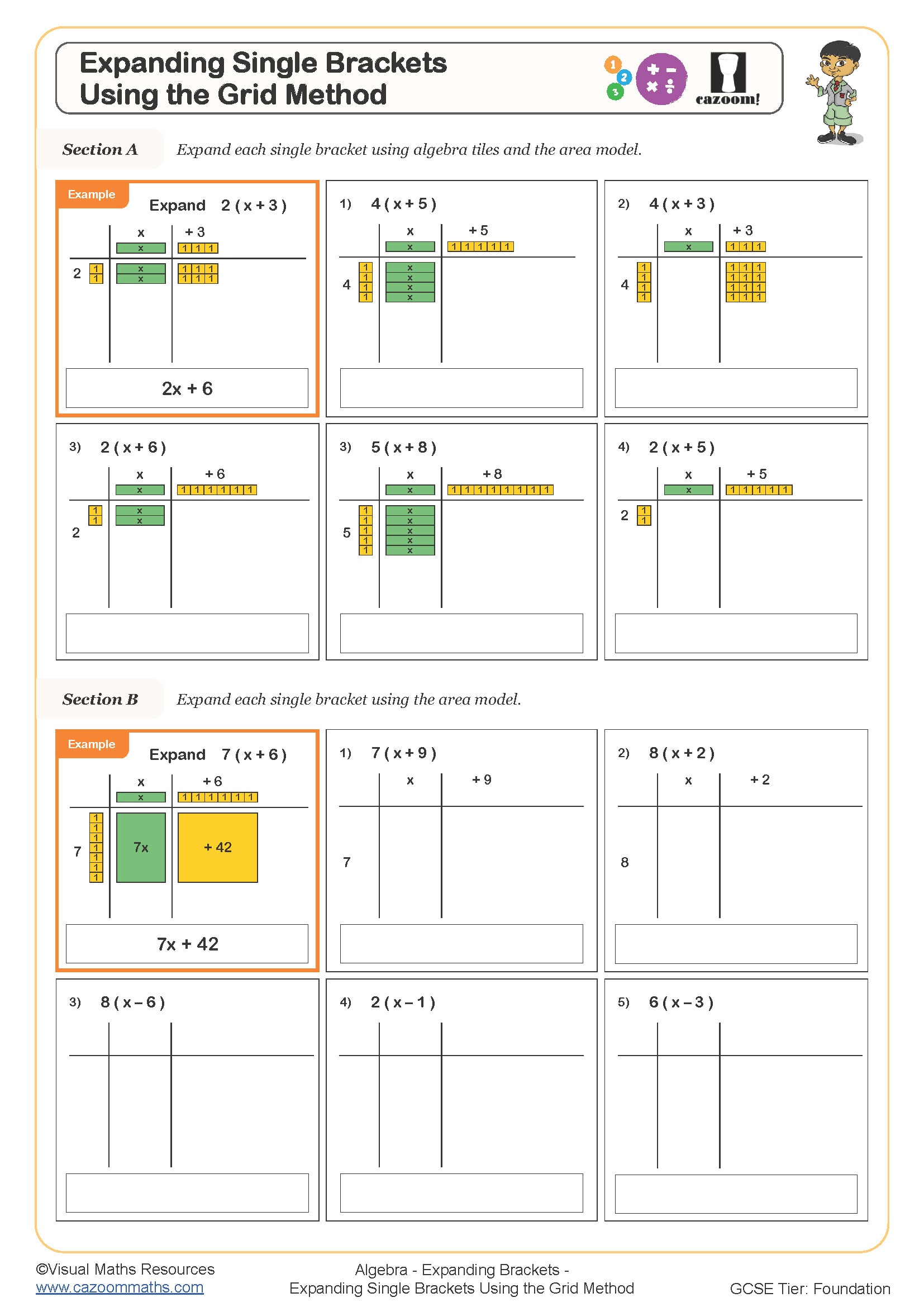
Expanding Single Brackets - Using the Grid Method
Introducing Algebra Tiles

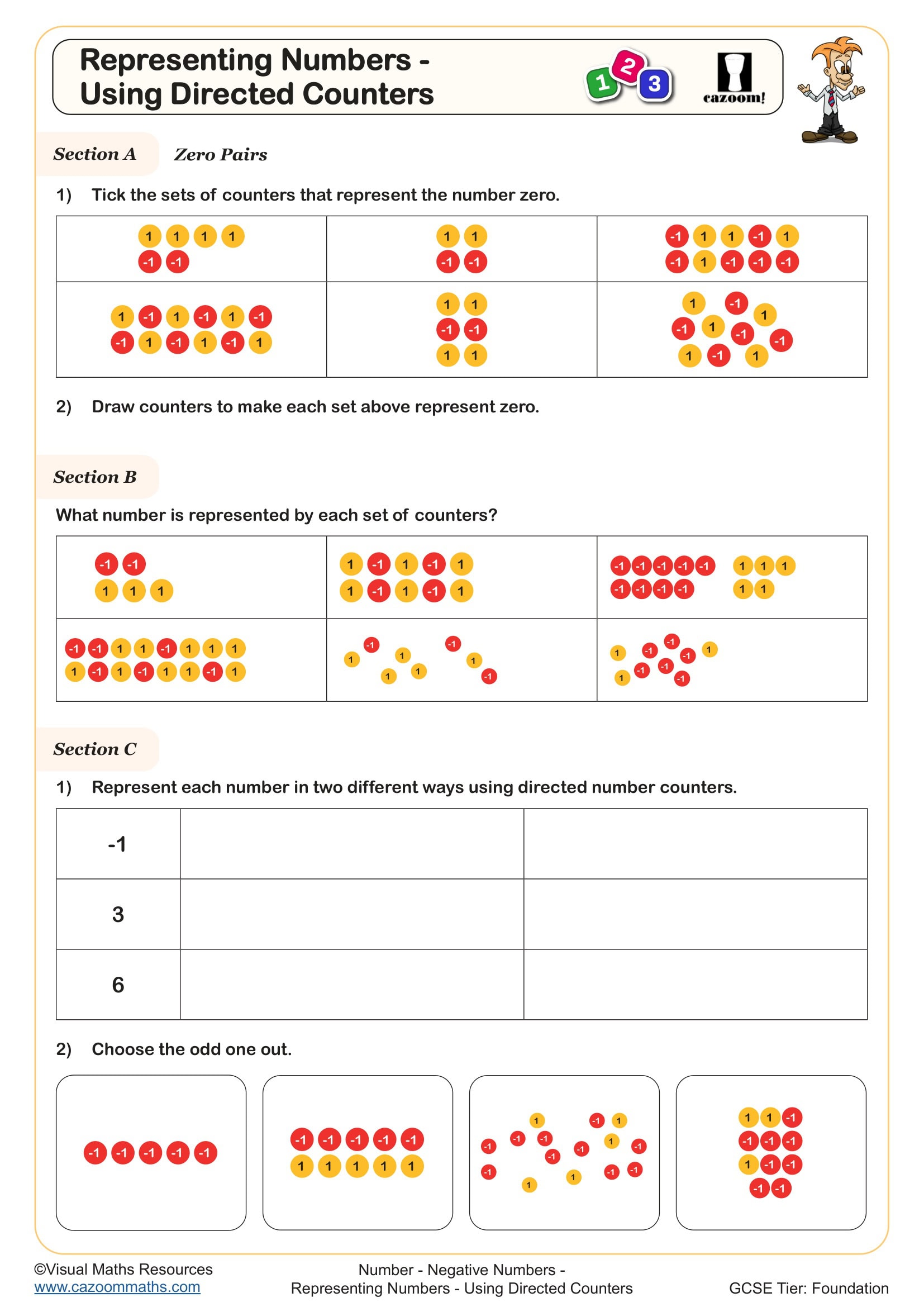
Representing Numbers - Using Directed Counters
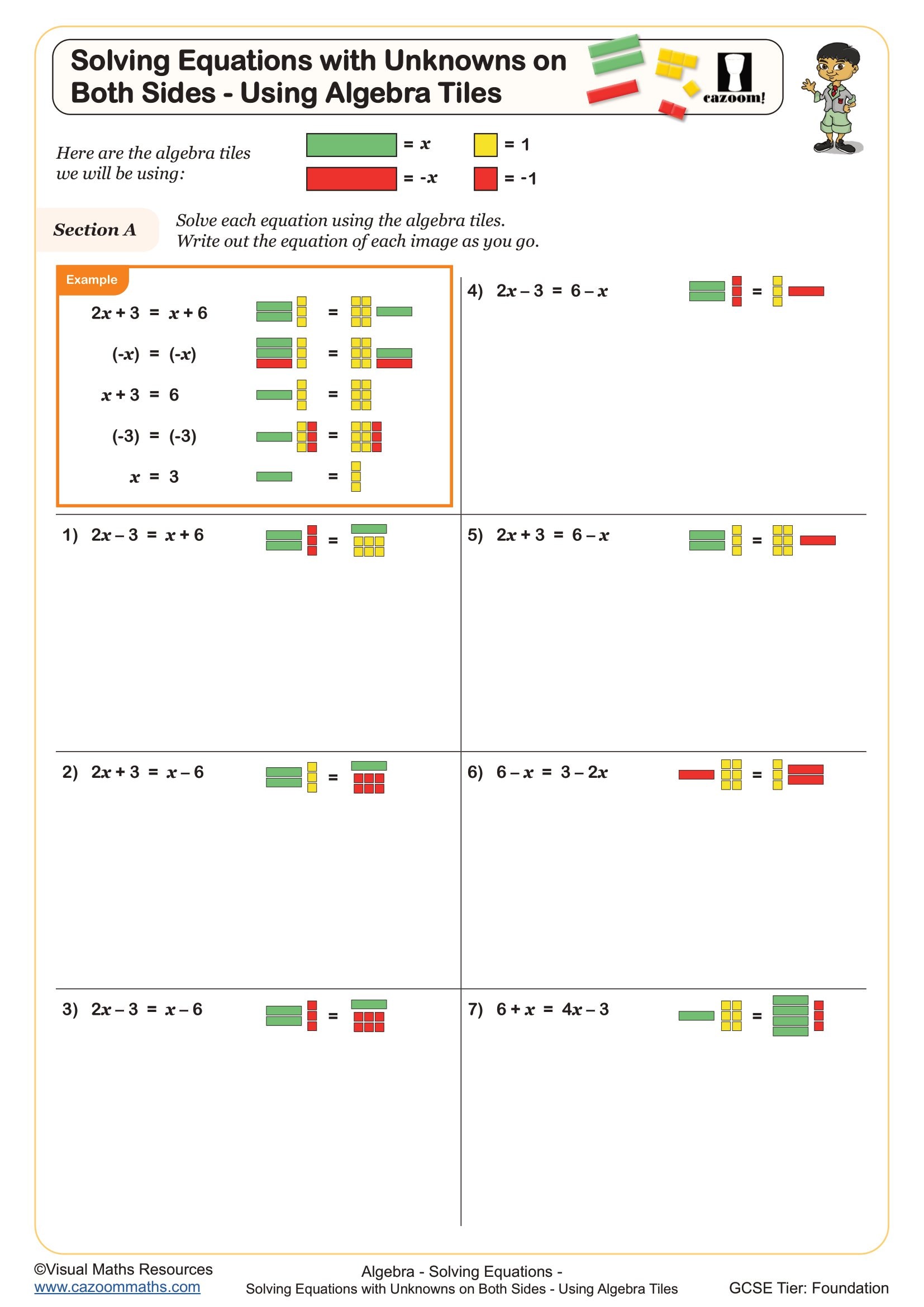
Solving Equations with Unknowns on Both Sides - Using Algebra Tiles
Solving One Step Equations with Algebra Tiles

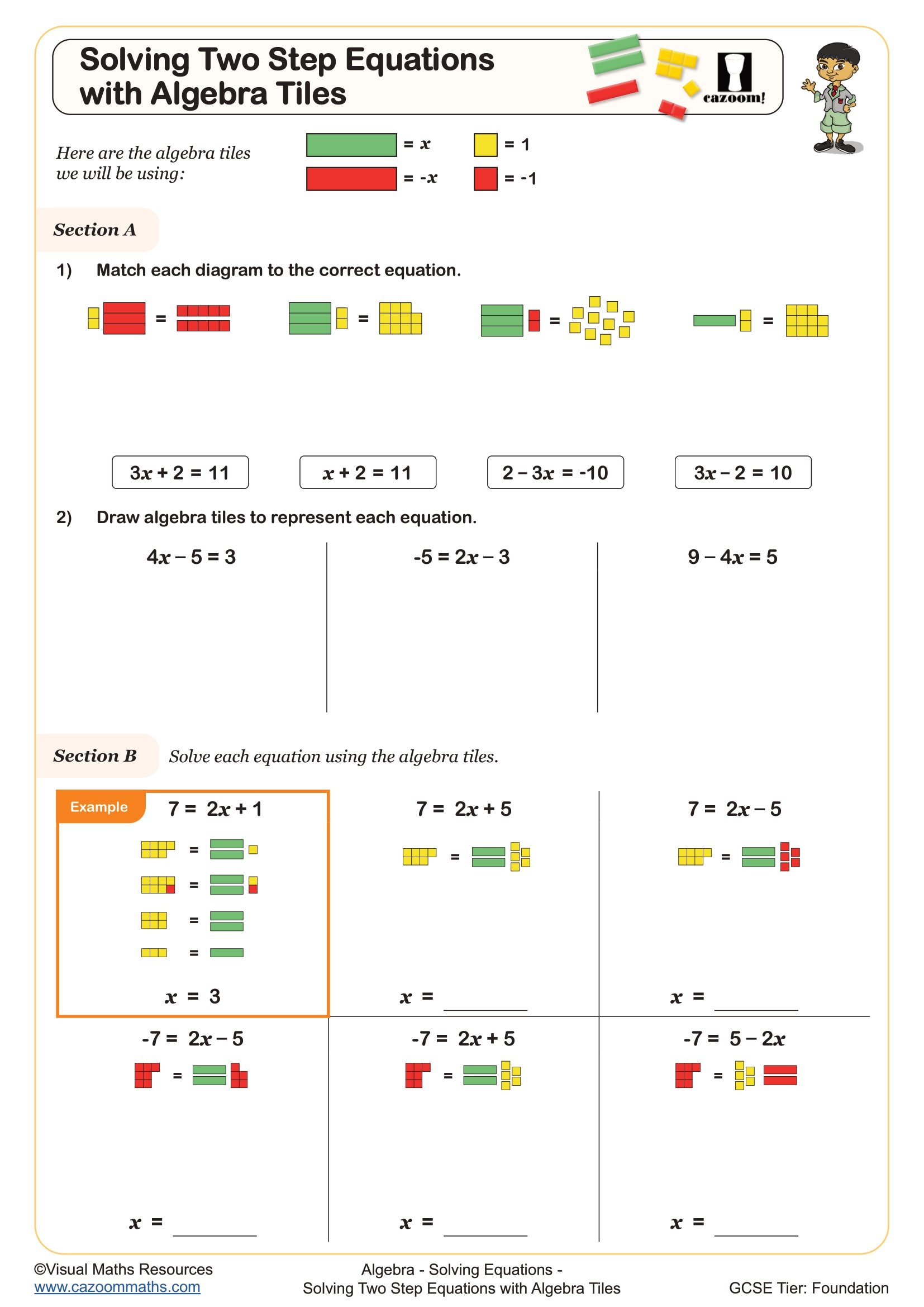
Solving Two Step Equations with Algebra Tiles
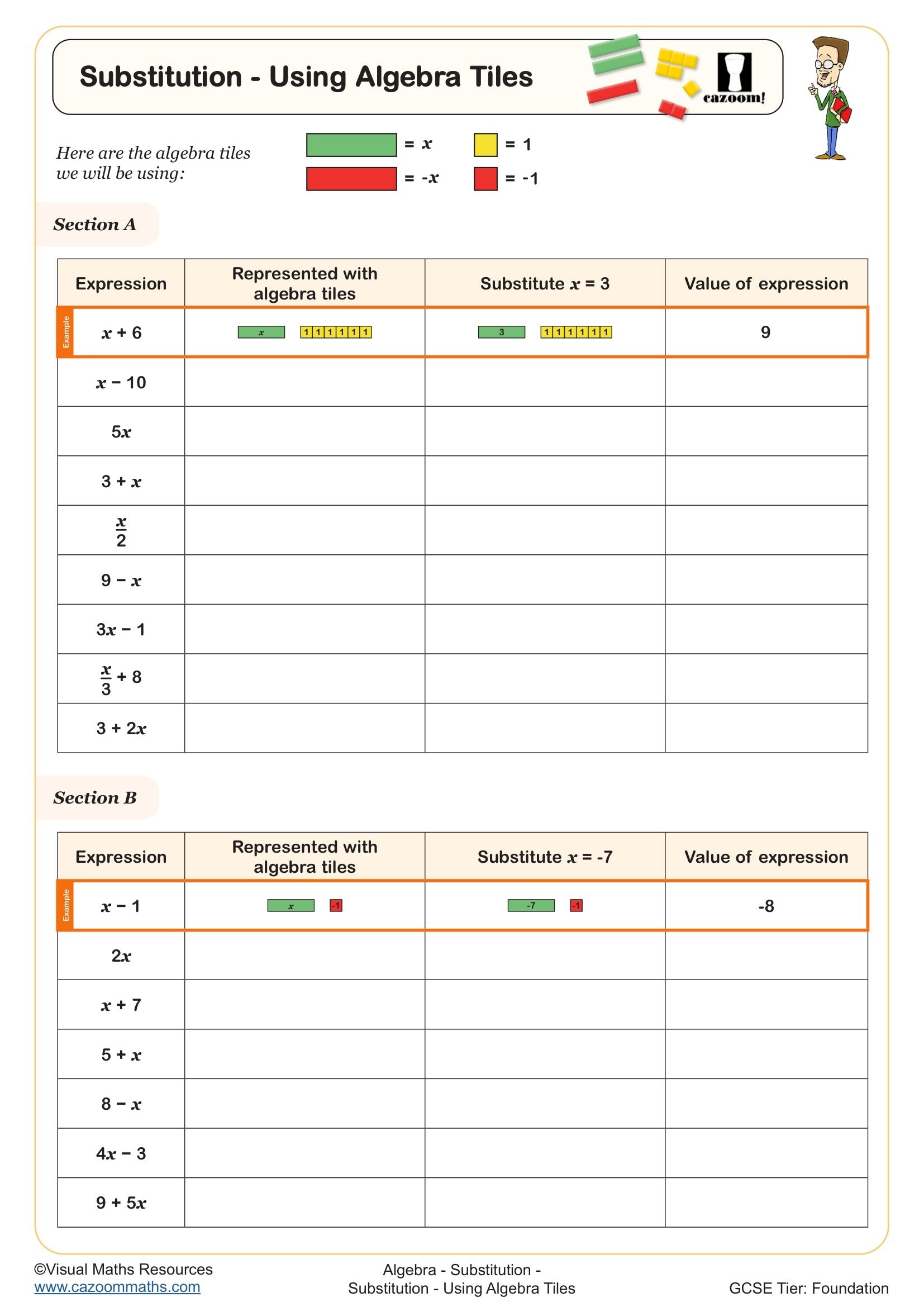
Substitution - Using Algebra Tiles
All worksheets are created by the team of experienced teachers at Cazoom Maths.
What are algebra tiles and how do KS3 algebra worksheets use them?
Algebra tiles are manipulatives that represent algebraic terms visually: typically, large rectangles represent x², smaller rectangles represent x, and small squares represent unit values of 1. Students arrange these tiles to model expressions like 3x + 2 or simplify by combining like terms. At KS3, ks3 algebra worksheets introduce algebra tiles as a bridge between arithmetic and abstract algebra, helping students understand why you can combine 2x and 3x but not 2x and 3y.
A common error occurs when students try to combine unlike tiles because they look similar in size on paper. Many teachers find that physically handling tiles (or drawing them with different colours) prevents this confusion. The visual representation makes it clear that an x-tile and a 1-tile represent fundamentally different quantities, reinforcing the concept of like terms before students move to purely symbolic manipulation in later years.
Which year groups use algebra tiles in the KS3 curriculum?
These algebra worksheets ks3 cover Year 7, Year 8, and Year 9, aligning with the National Curriculum's progression through algebraic thinking. Year 7 students typically use algebra tiles to understand what a variable represents and to model simple expressions. Year 8 work extends to simplifying more complex expressions with multiple terms and introducing negative tiles to represent subtraction or negative coefficients.
By Year 9, students use algebra tiles to model and solve equations, physically balancing both sides to understand why operations must be performed equally. The progression moves from concrete manipulation toward abstract symbolic reasoning, with tiles serving as a support structure that students gradually rely on less. Teachers often notice that even confident Year 9 students benefit from returning to tiles when encountering quadratic expressions or factorisation for the first time.
How do algebra tiles help with understanding unknowns and simplification?
Algebra tiles make the concept of an unknown tangible by representing it as a physical object with consistent dimensions. When simplifying expressions, students group tiles of the same type together, physically demonstrating that 2x + 3x becomes 5x because you have five x-tiles in total. This concrete action builds understanding before introducing the abstract rule that you add coefficients of like terms.
This skill connects directly to coding and computer science, where variables store unknown values that change during program execution. Engineers use similar visual modelling when working with equations that represent physical quantities like force or distance. Understanding that variables represent measurable quantities, not just letters to manipulate, helps students later when applying algebra to calculate voltages in circuits or optimise dimensions in design projects where unknowns have real-world meaning.
How can teachers use these algebra tiles worksheets effectively in lessons?
The worksheets provide structured practice that moves from guided examples with visual tile representations to questions where students sketch their own tile arrangements before writing algebraic solutions. This scaffolding helps students develop the mental imagery needed to work algebraically without physical manipulatives. Early questions typically show tiles already arranged, asking students to write the corresponding expression, whilst later questions reverse this by providing expressions for students to model.
Teachers often use these worksheets during initial teaching to accompany physical or digital tile sets, then return to them during intervention sessions when students struggle with abstract algebra later in KS3. They work well for paired discussion where students explain their tile arrangements to each other, verbalising mathematical reasoning. The answer sheets allow for self-marking during revision or enable teaching assistants to support small groups without needing subject-specialist knowledge of algebraic manipulation techniques.