KS3 Lines and Angles Worksheets
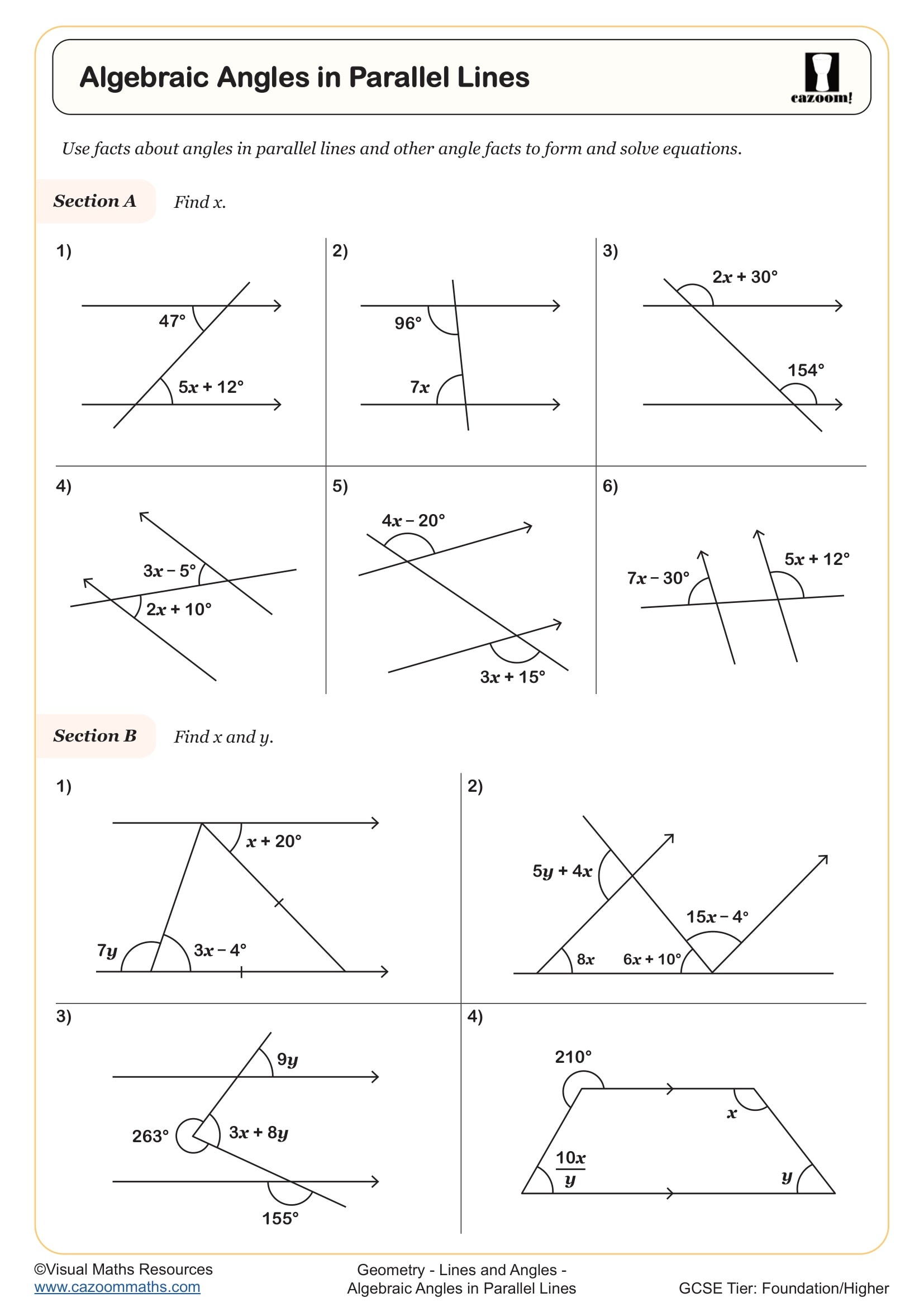
Algebraic Angles in Parallel Lines
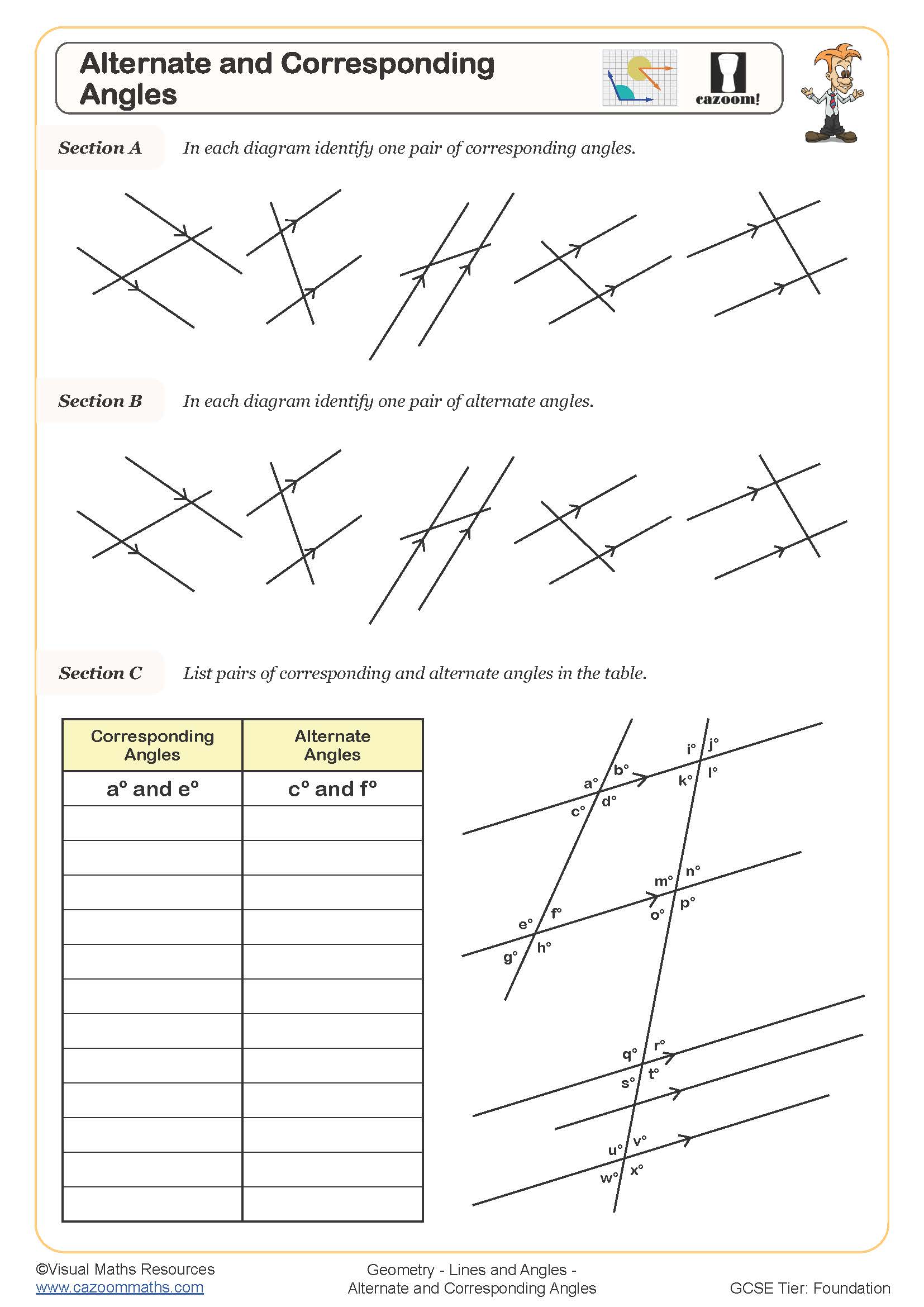
Alternate and Corresponding Angles (A)
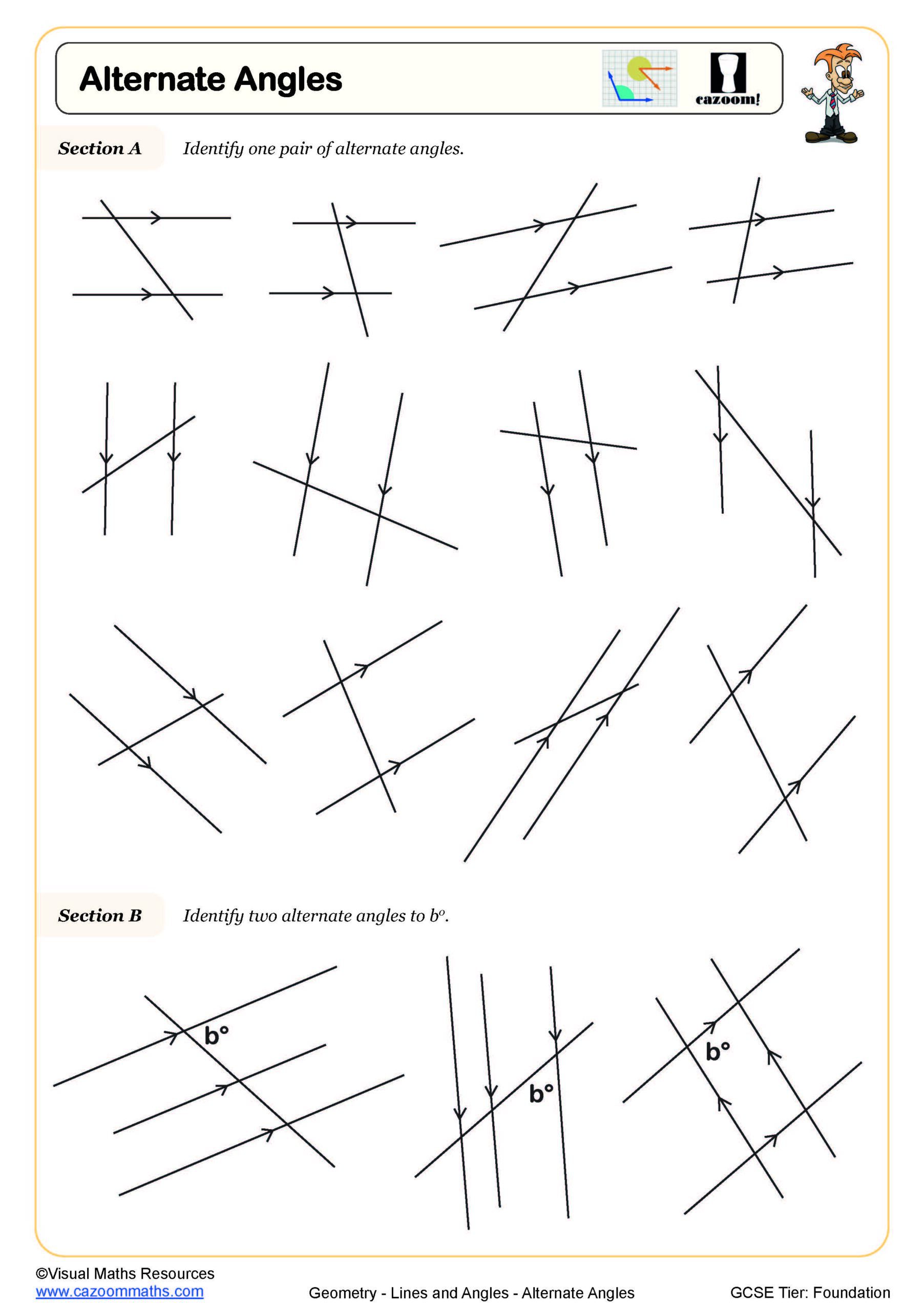
Alternate Angles
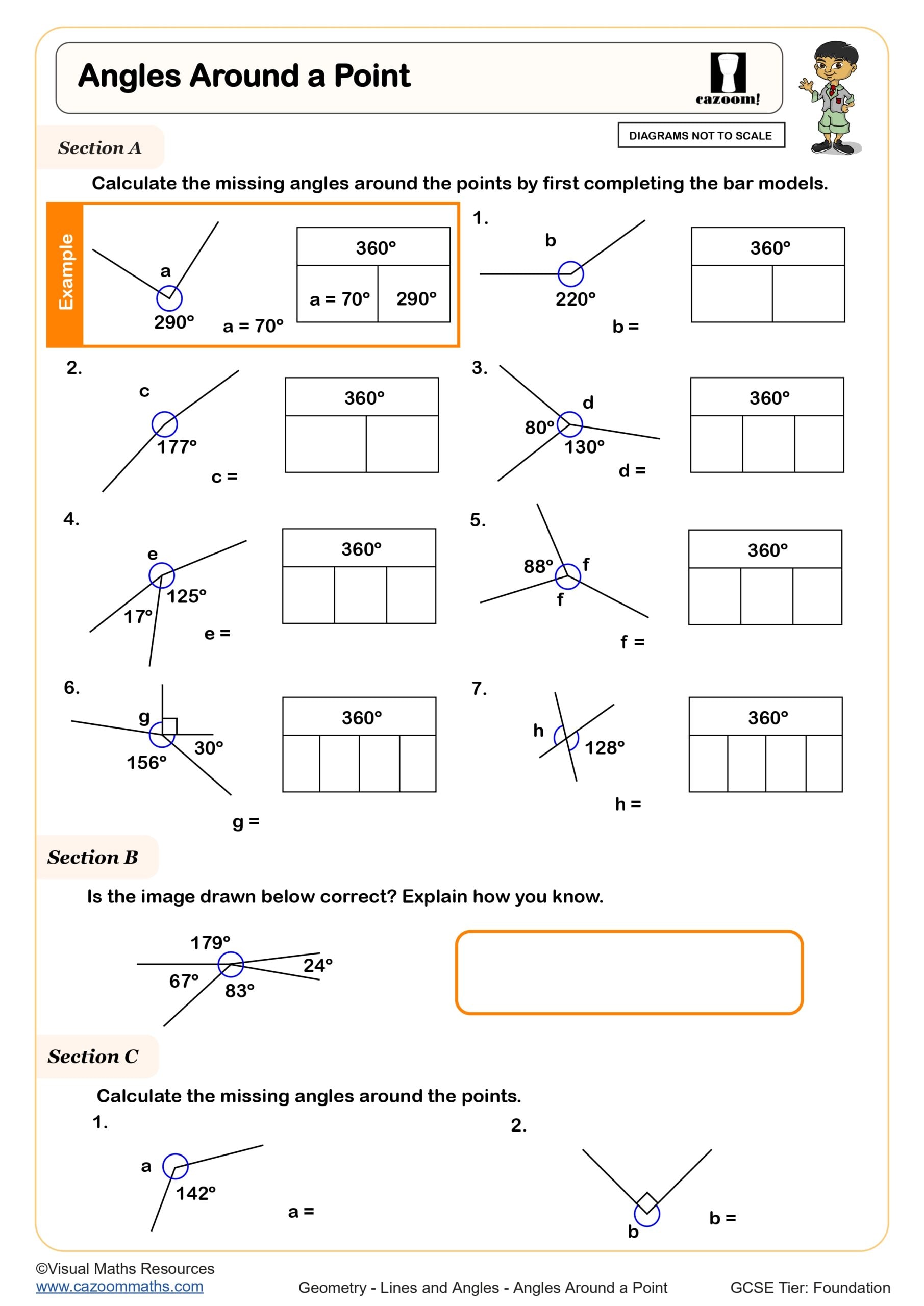
Angles Around a Point
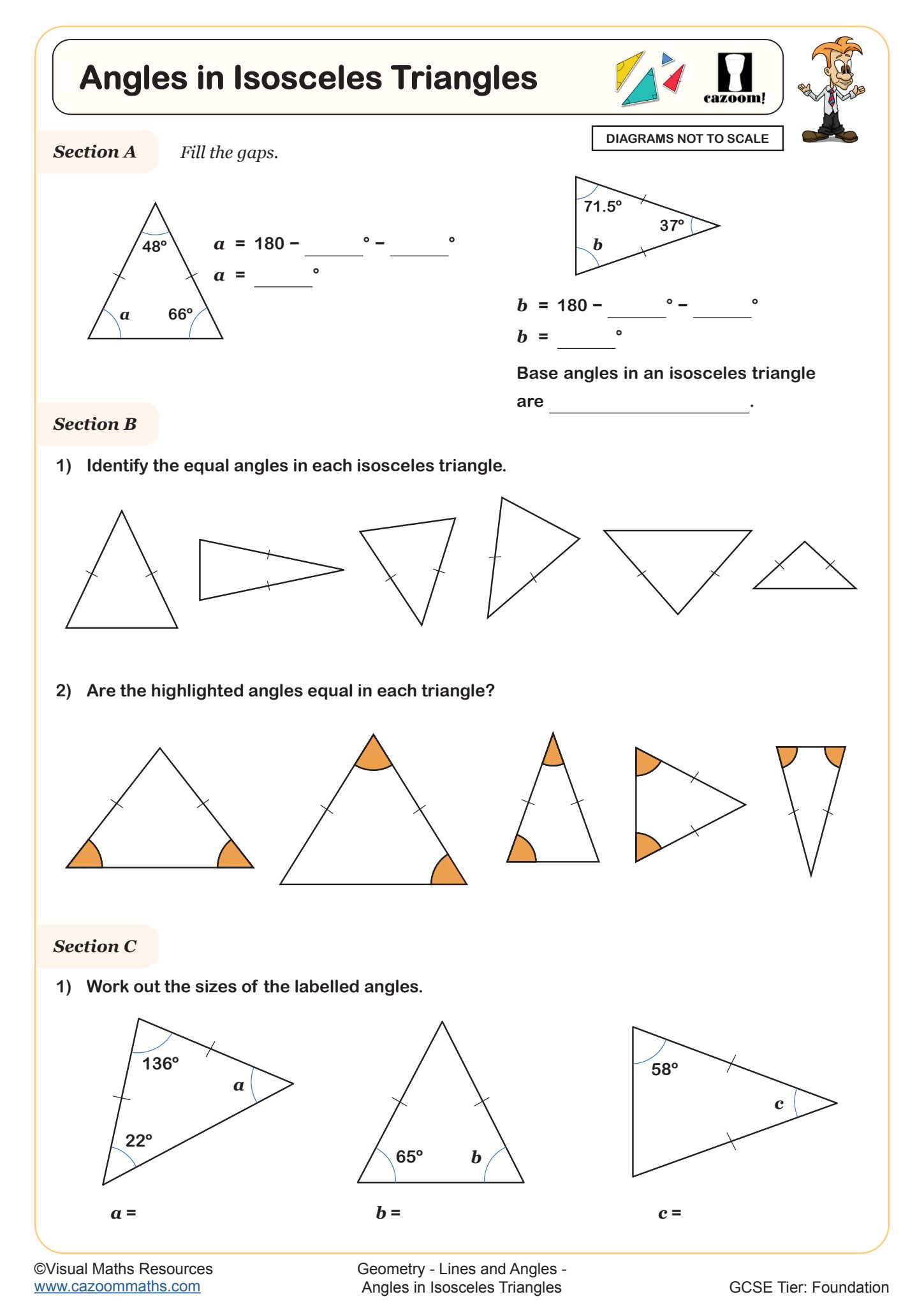
Angles in Isosceles Triangles
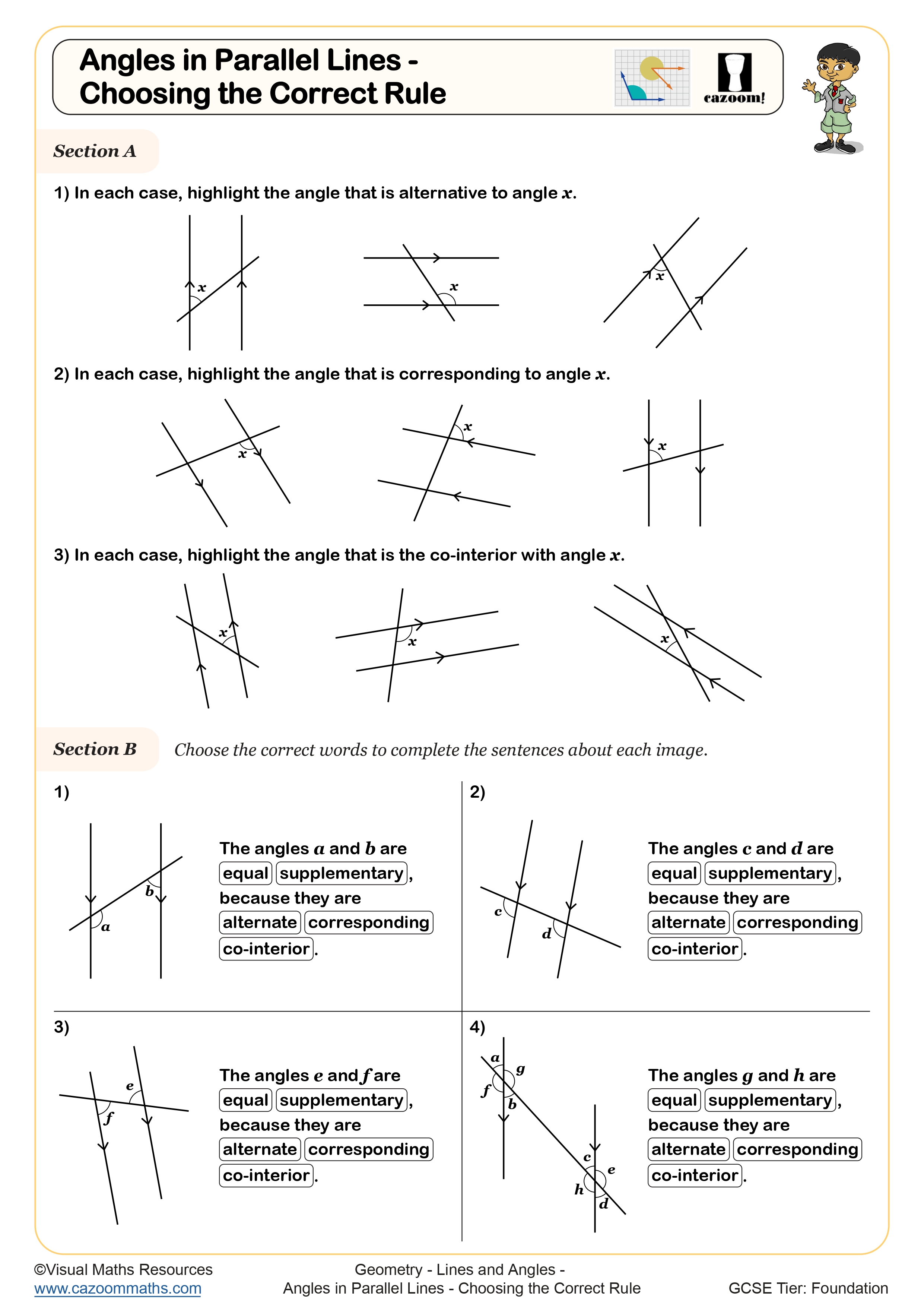
Angles in Parallel Lines - Choosing the Correct Rule
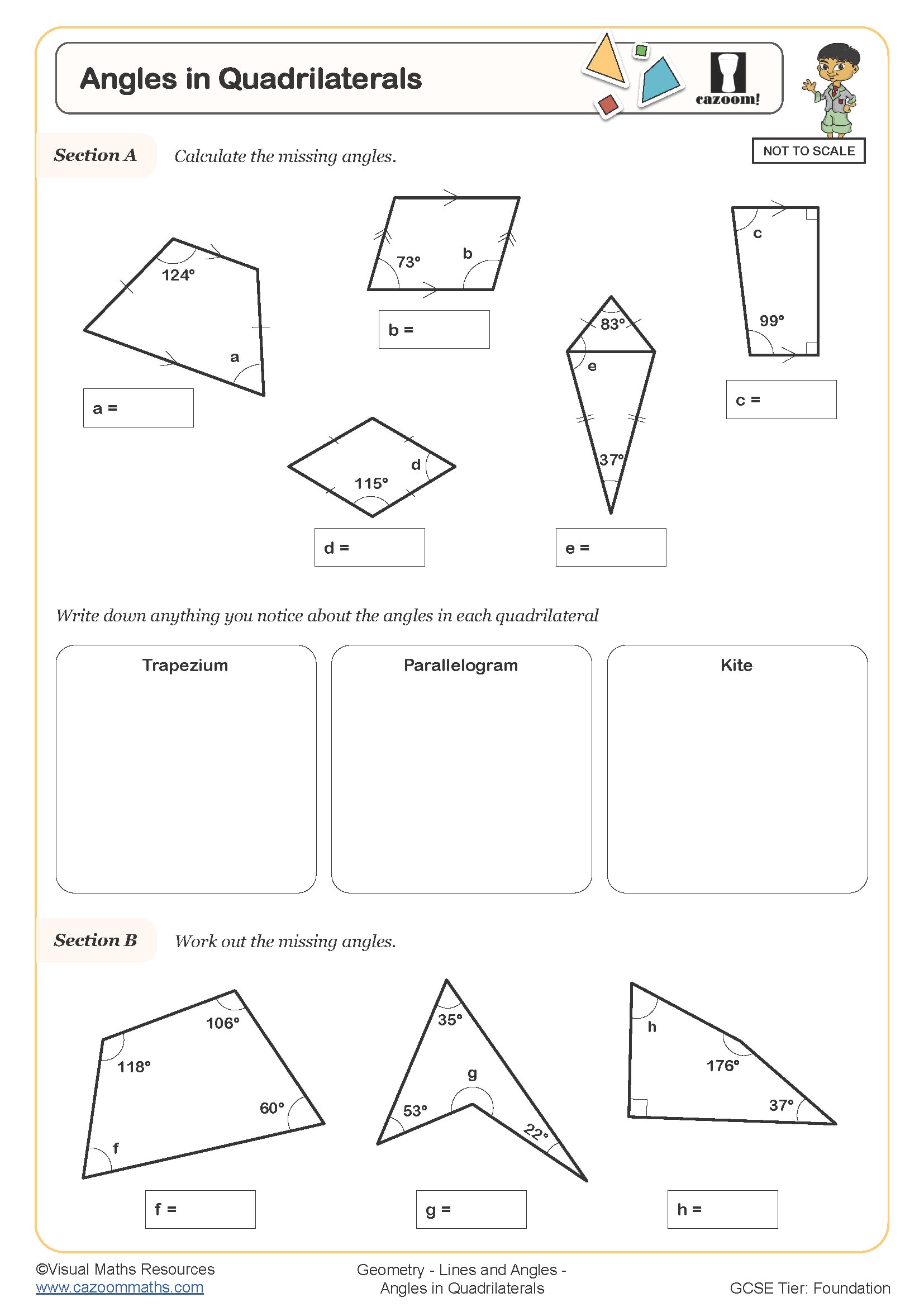
Angles in Quadrilaterals
Angles in Triangles
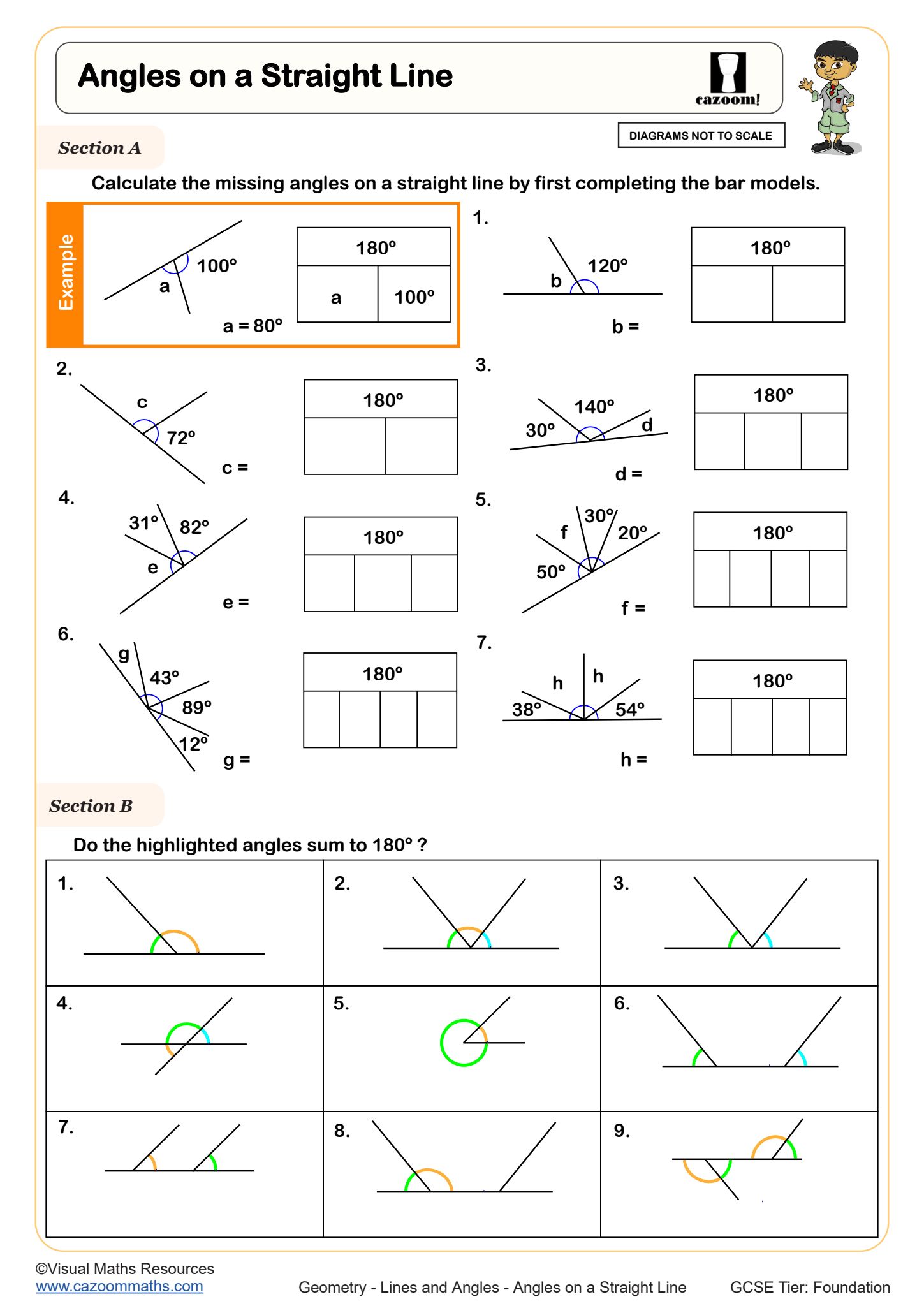
Angles on a Straight Line
Angles on Parallel Lines (A)
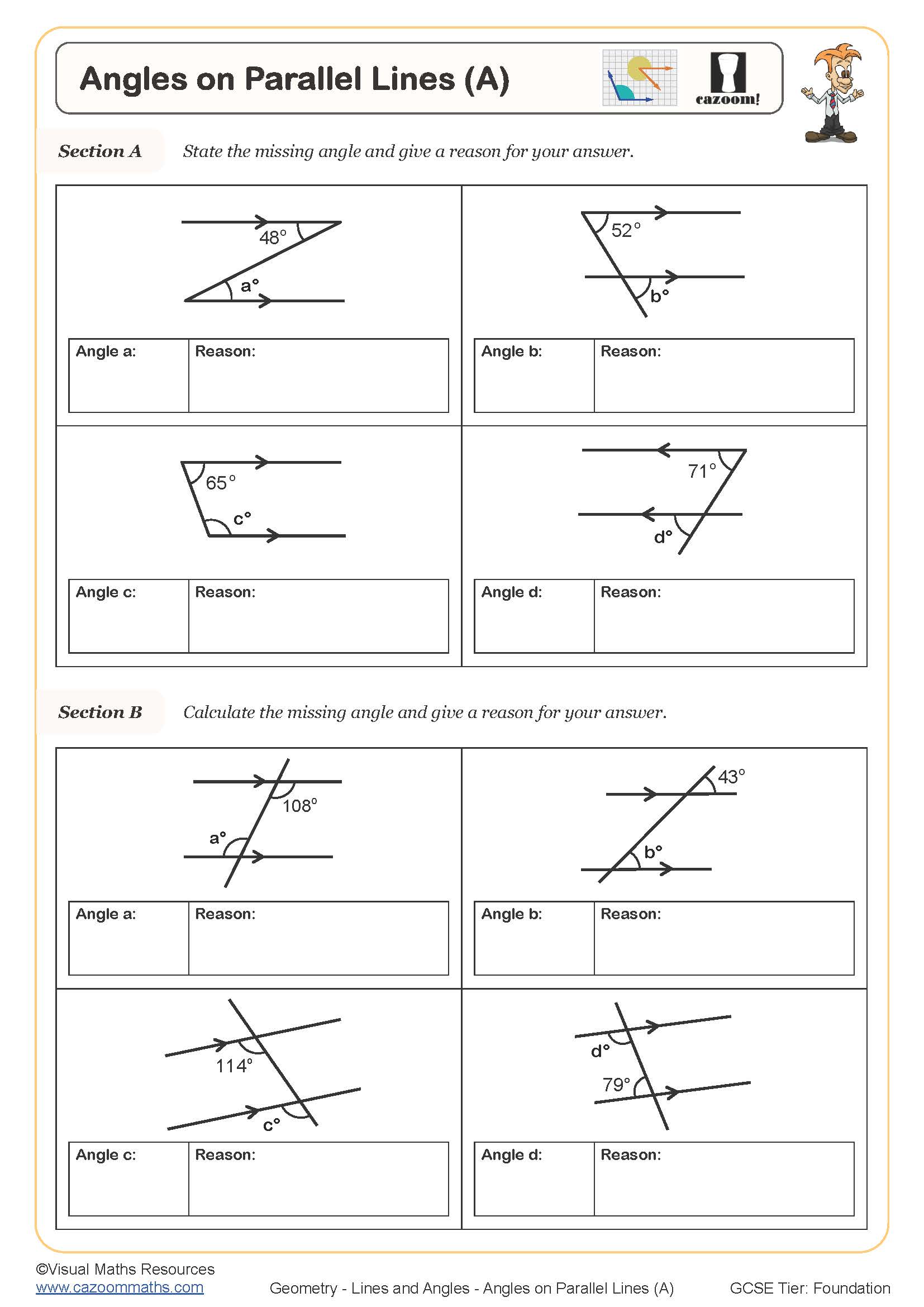
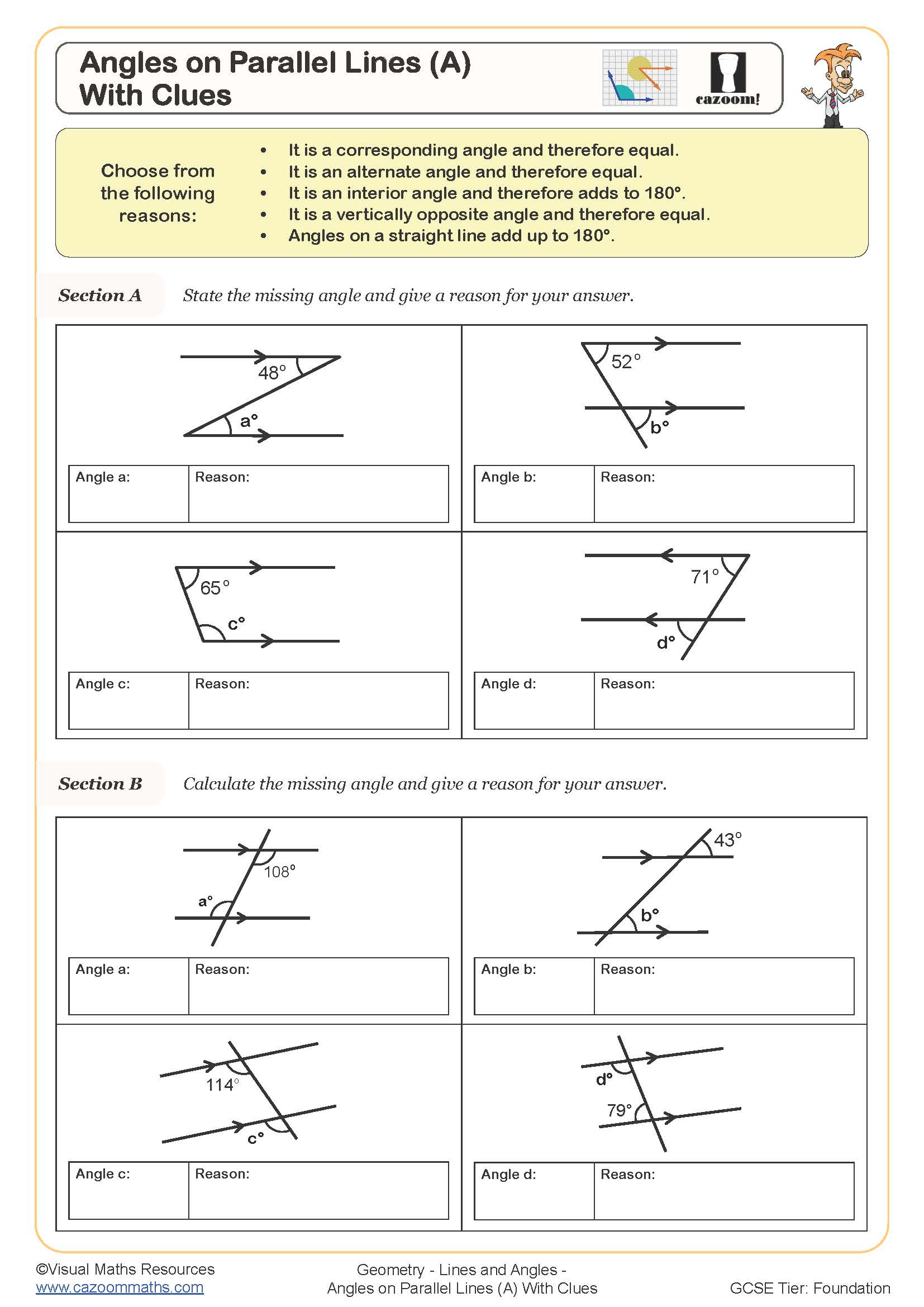
Angles on Parallel Lines (A) (With Clues)
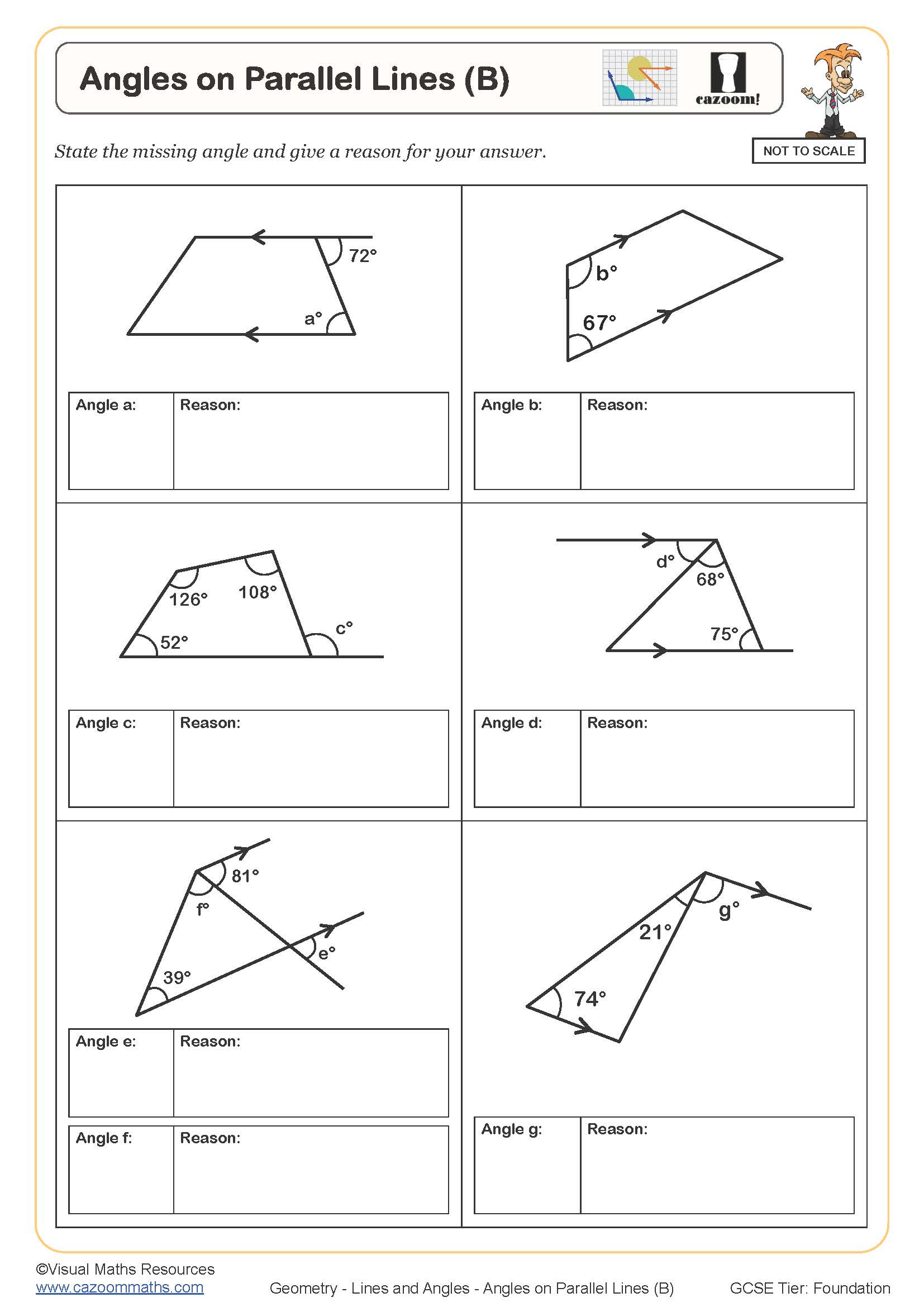
Angles on Parallel Lines (B)
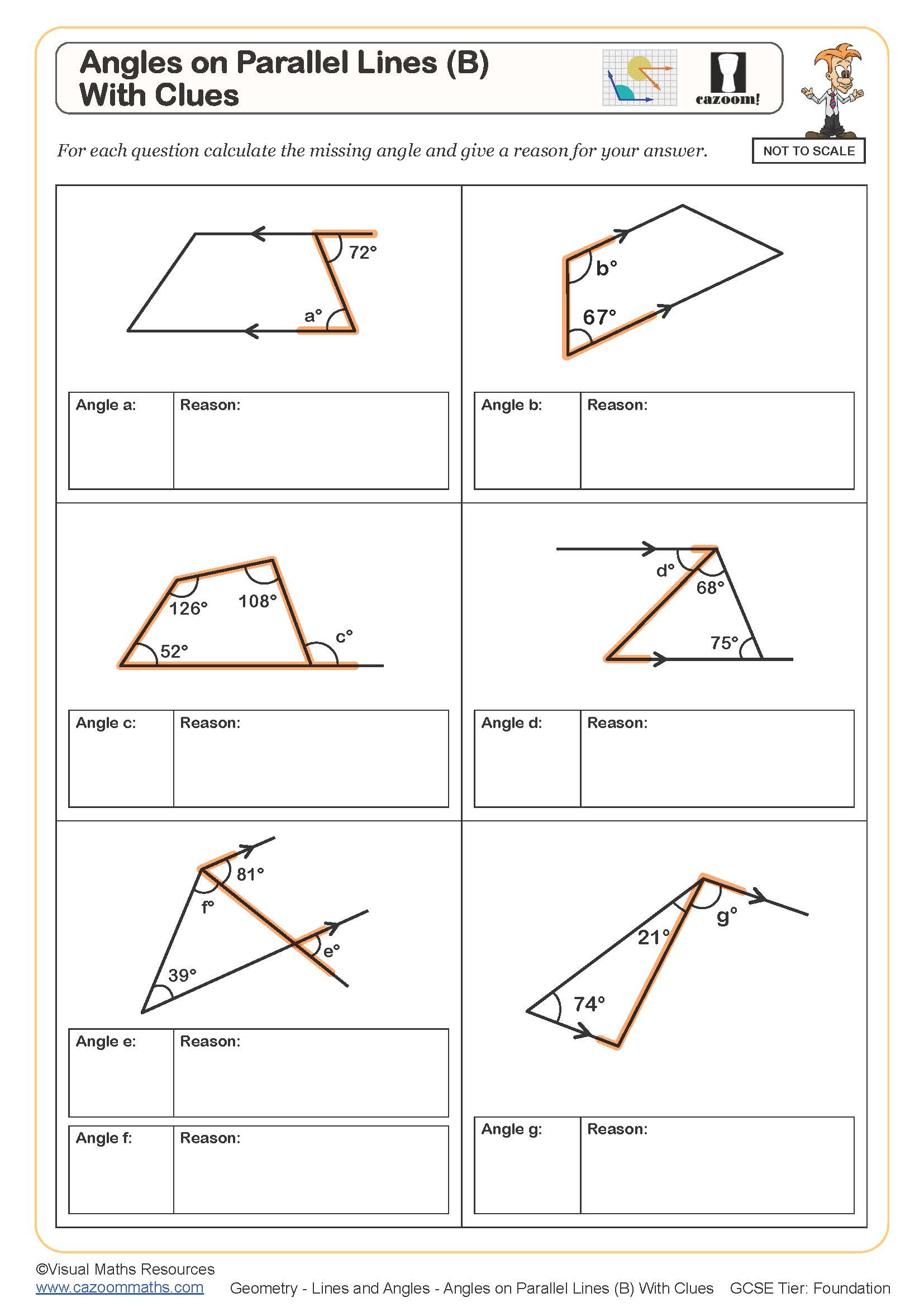
Angles on Parallel Lines (B) (With Clues)
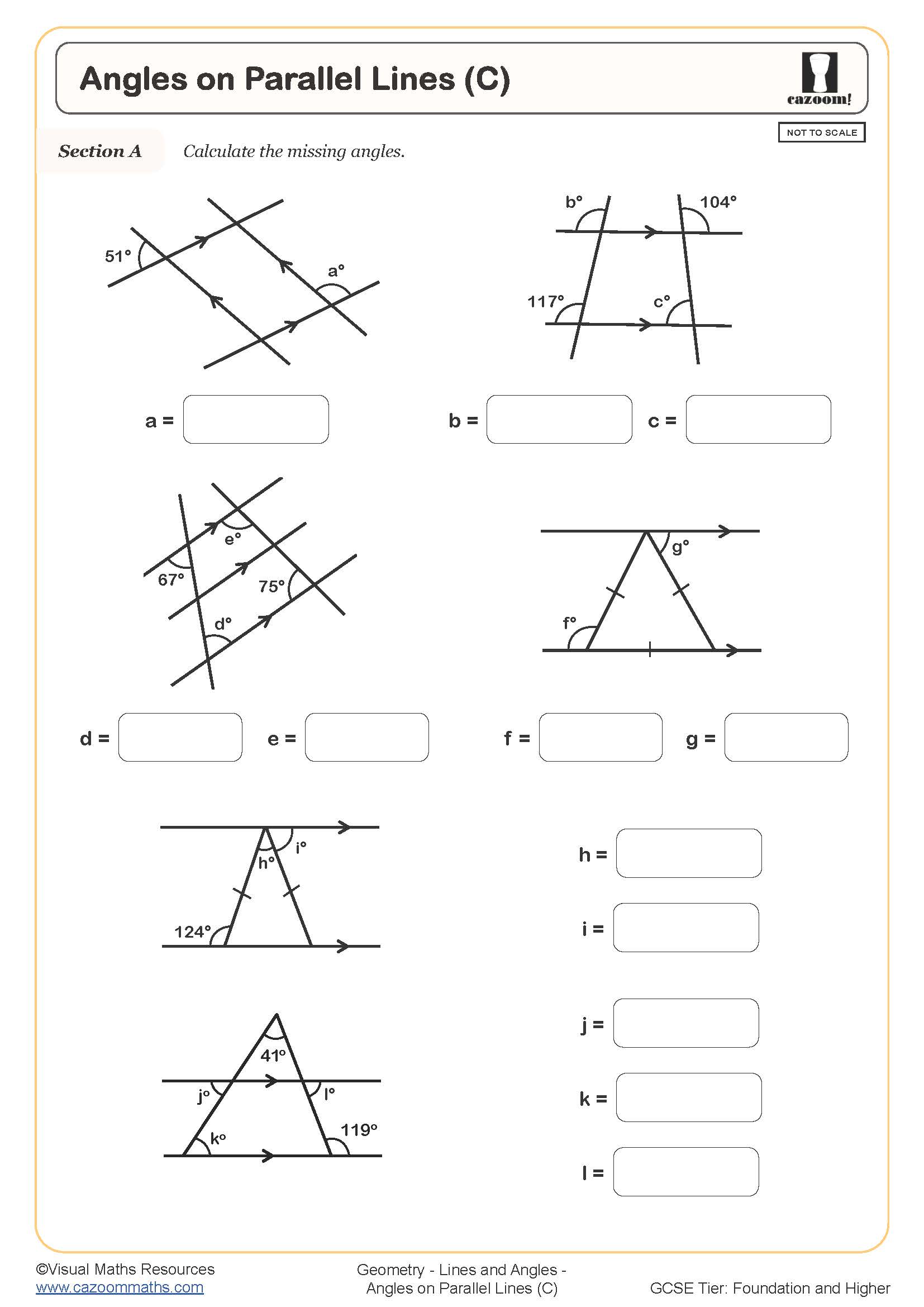
Angles on Parallel Lines (C)
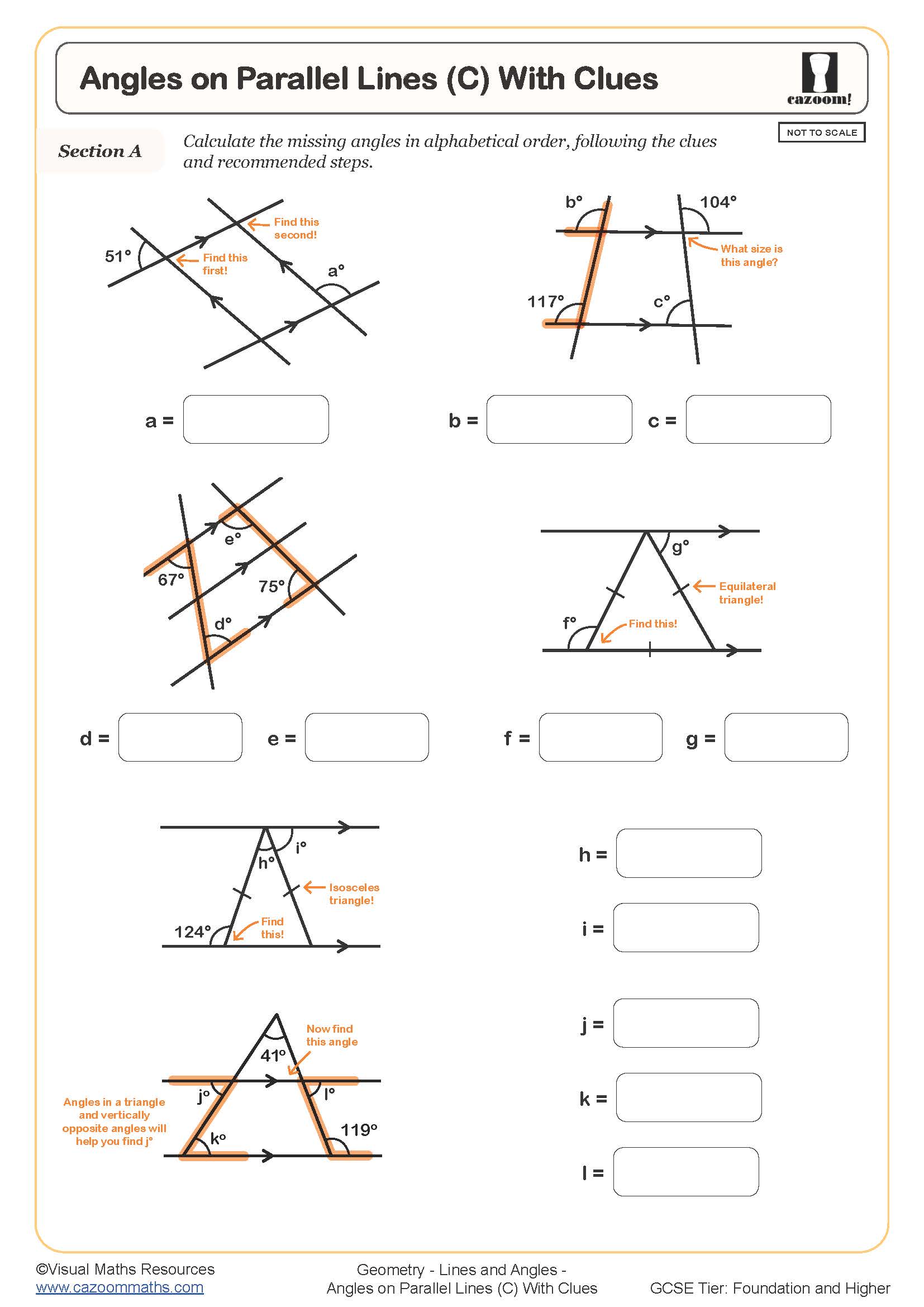
Angles on Parallel Lines (C) (With Clues)
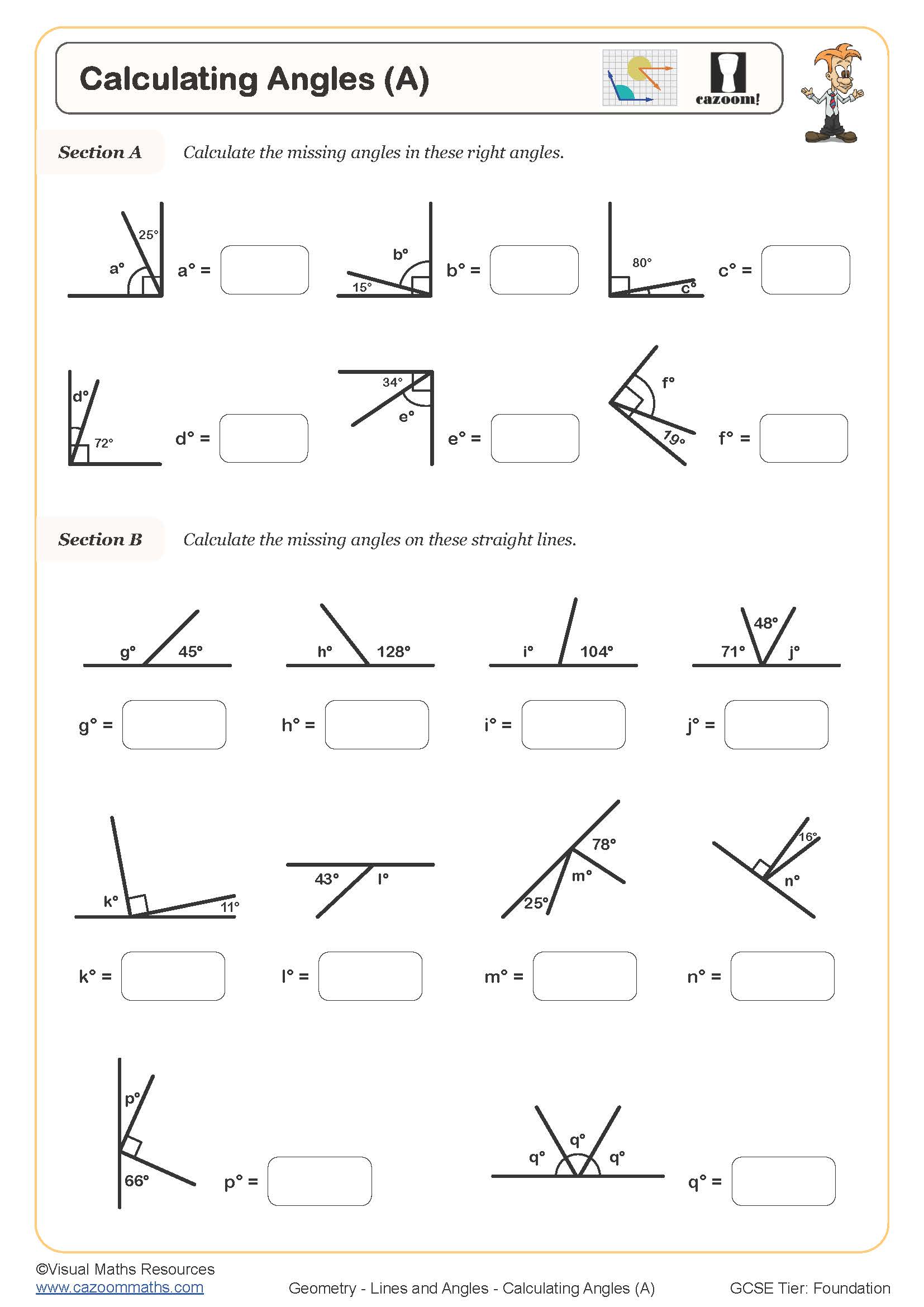
Calculating Angles (A)
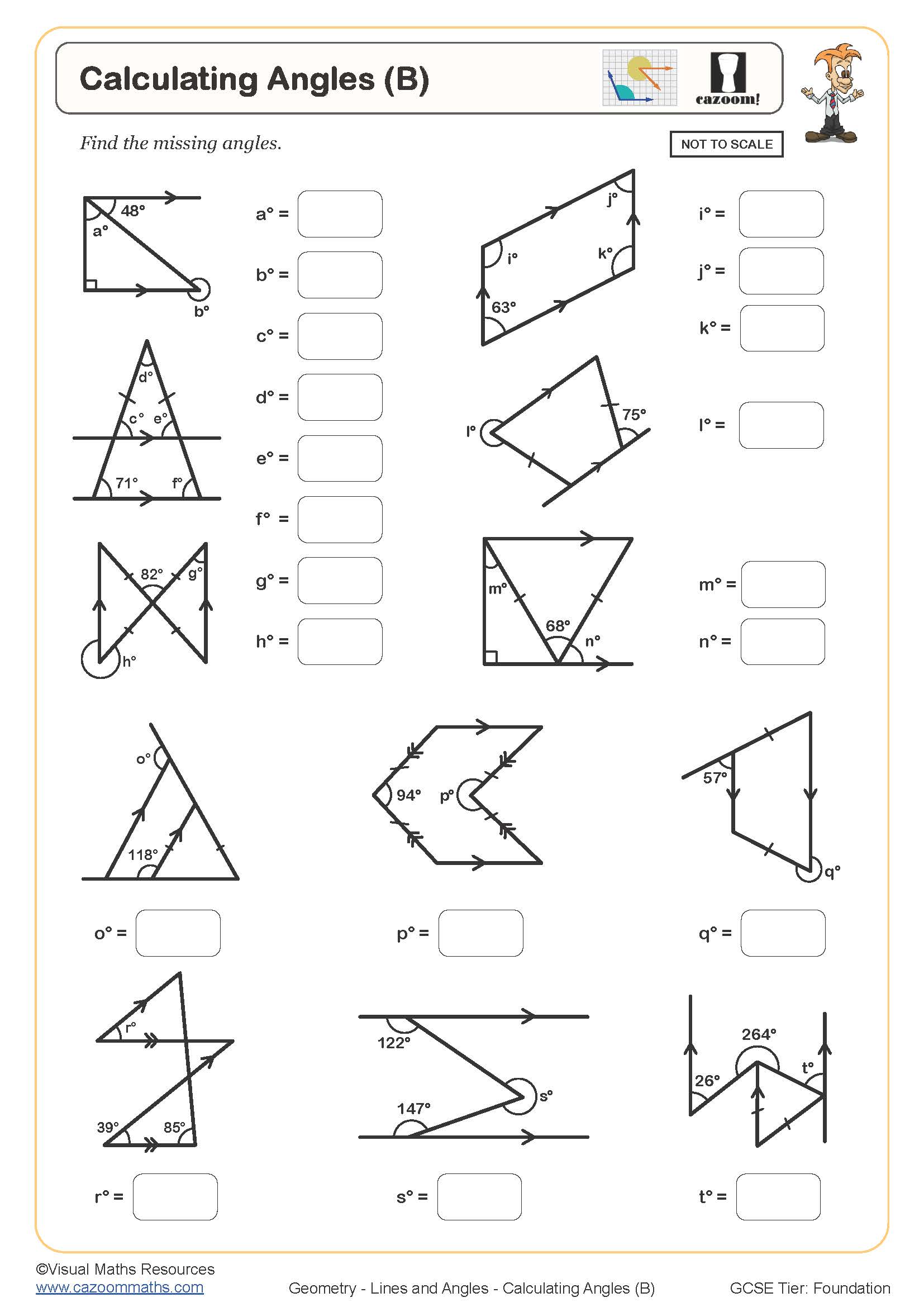
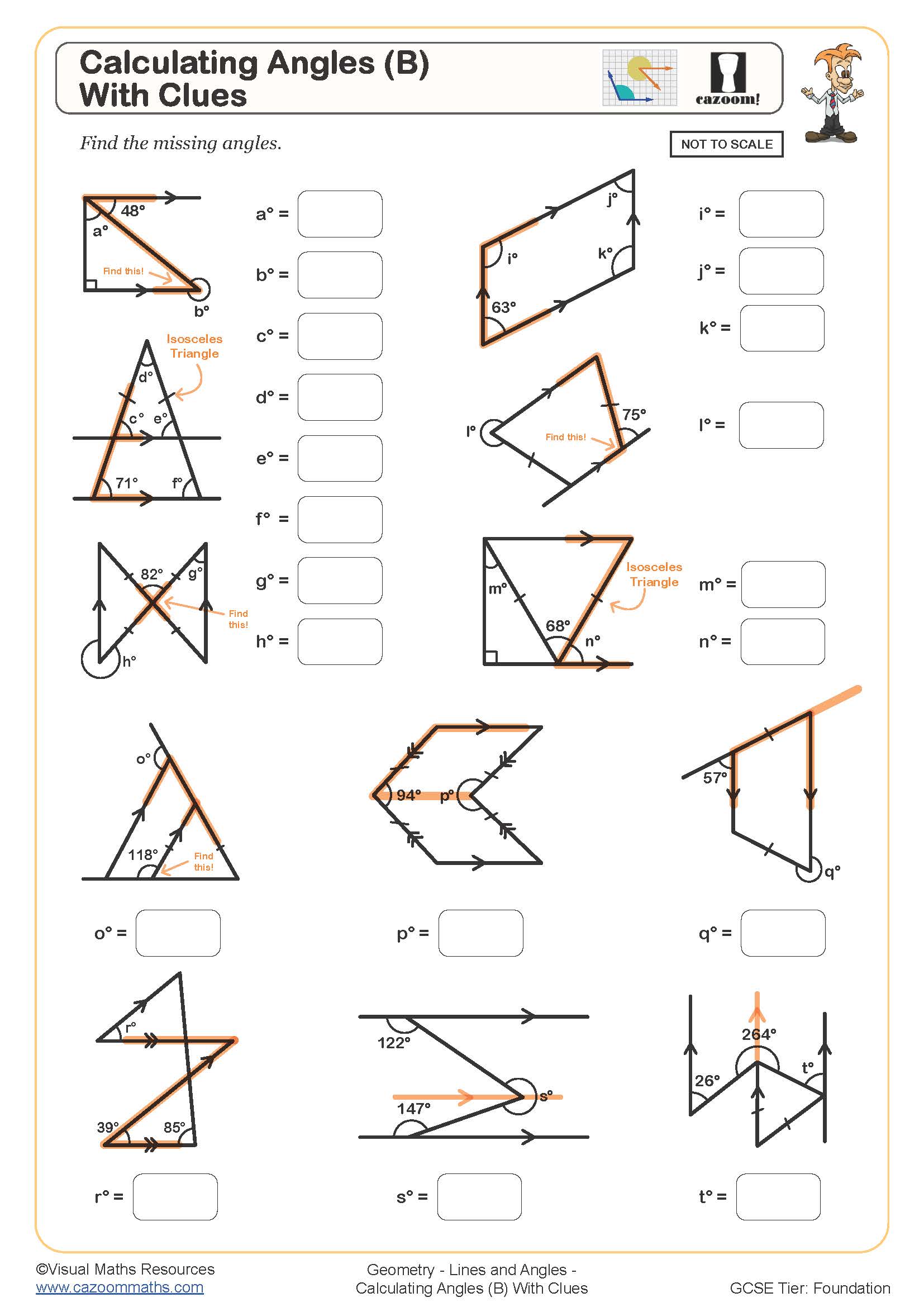
Calculating Angles (B)
Calculating Angles (B) (With Clues)
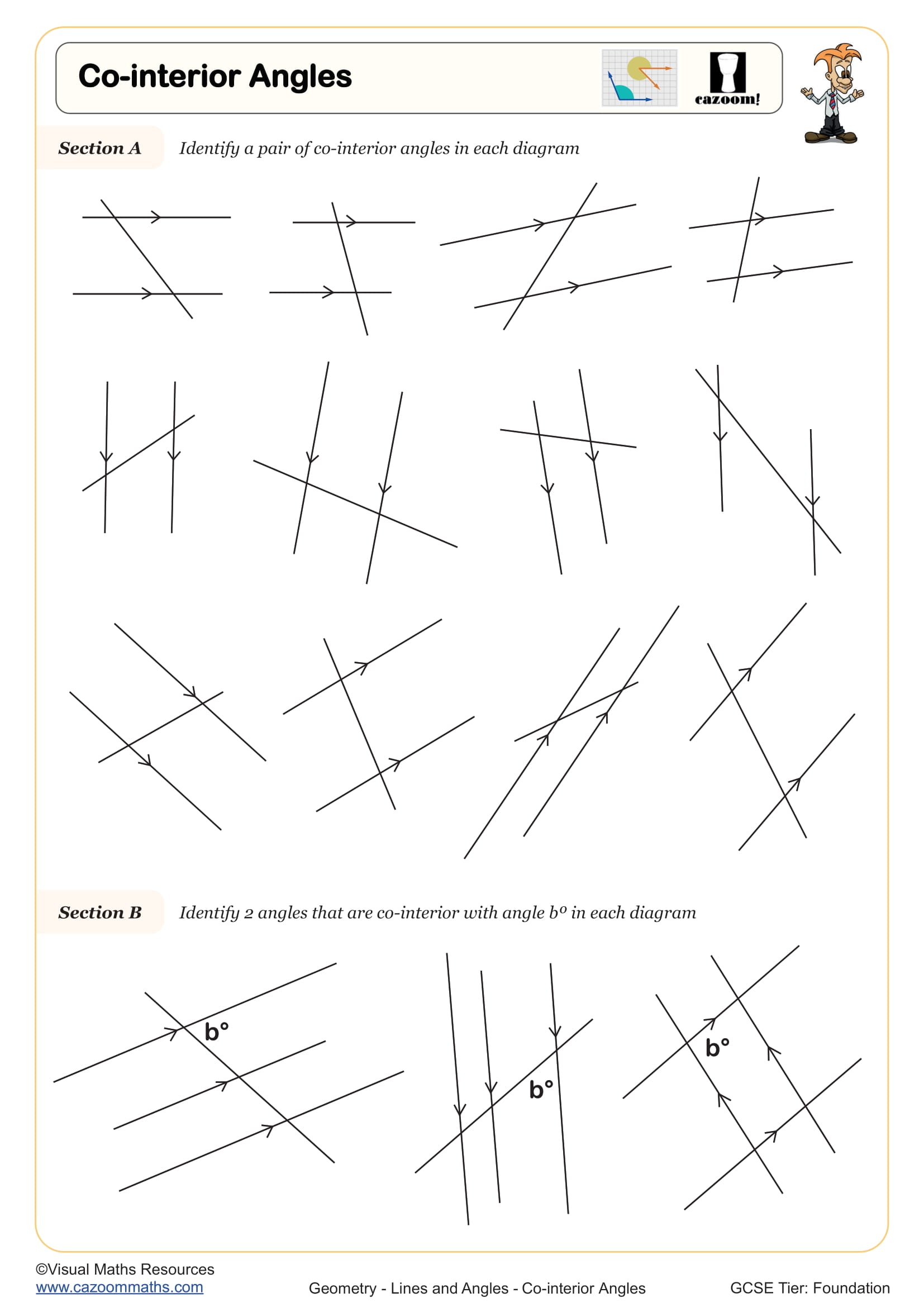
Co-interior Angles
Corresponding Angles
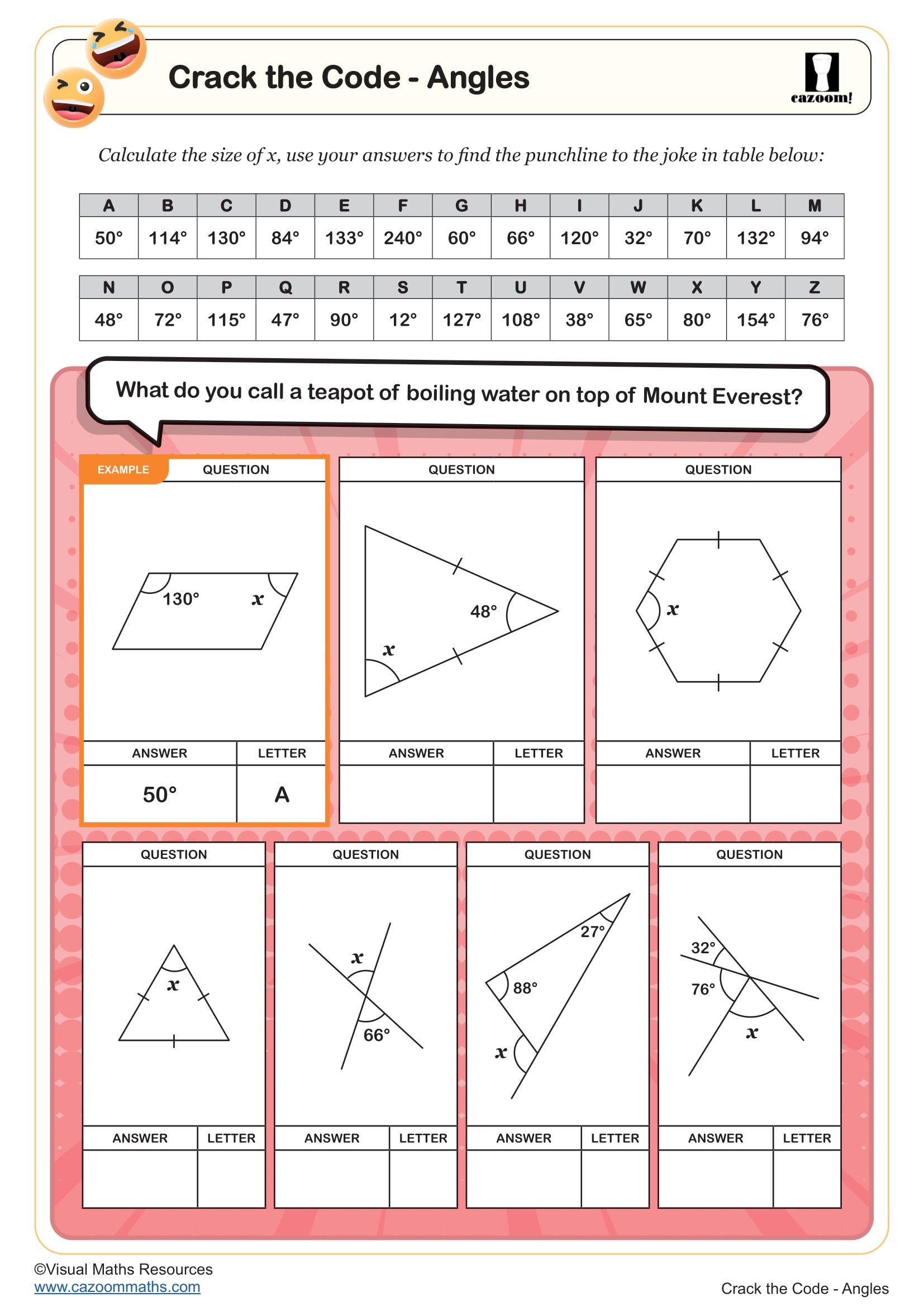
Crack the Code - Angles
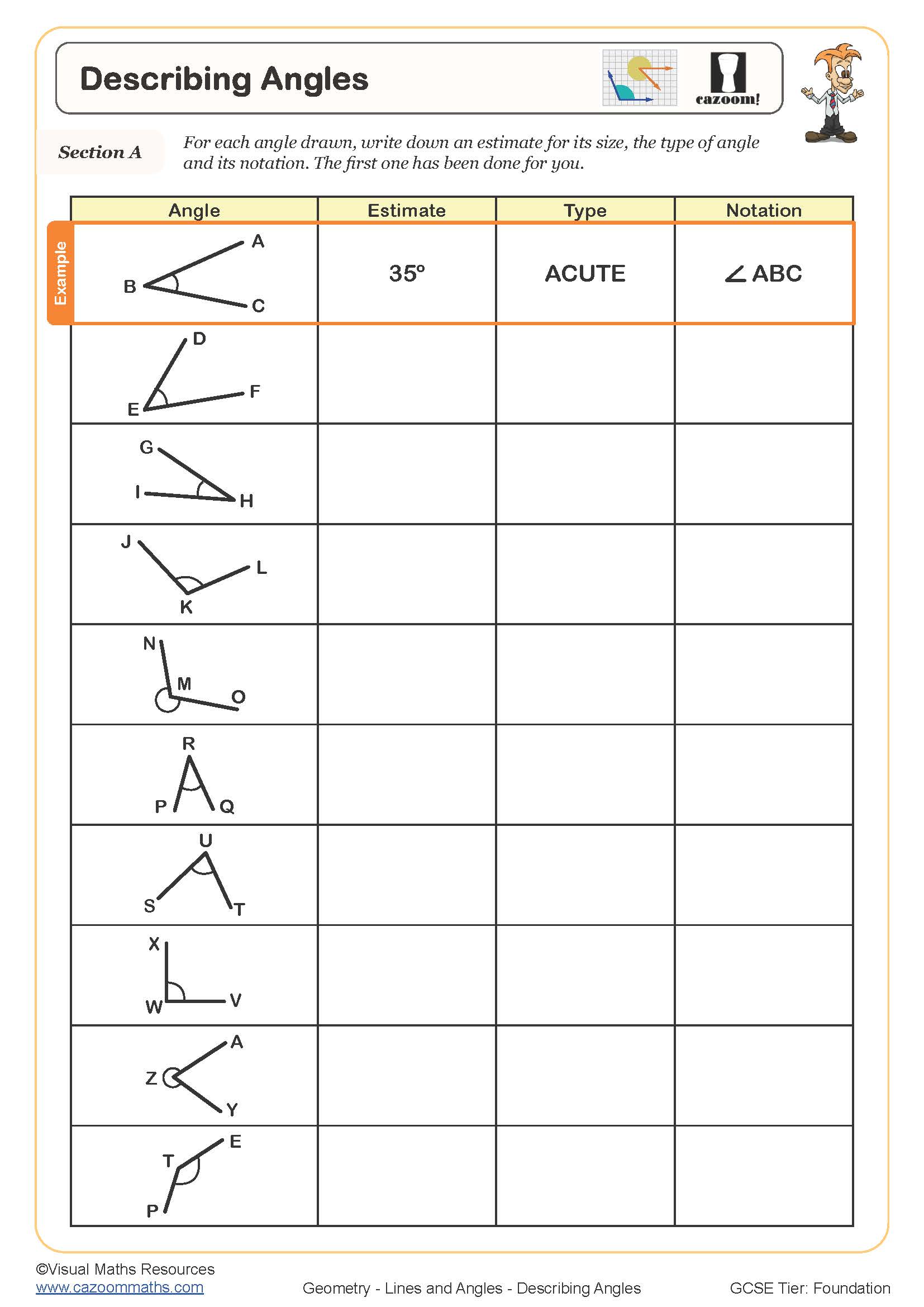
Describing Angles
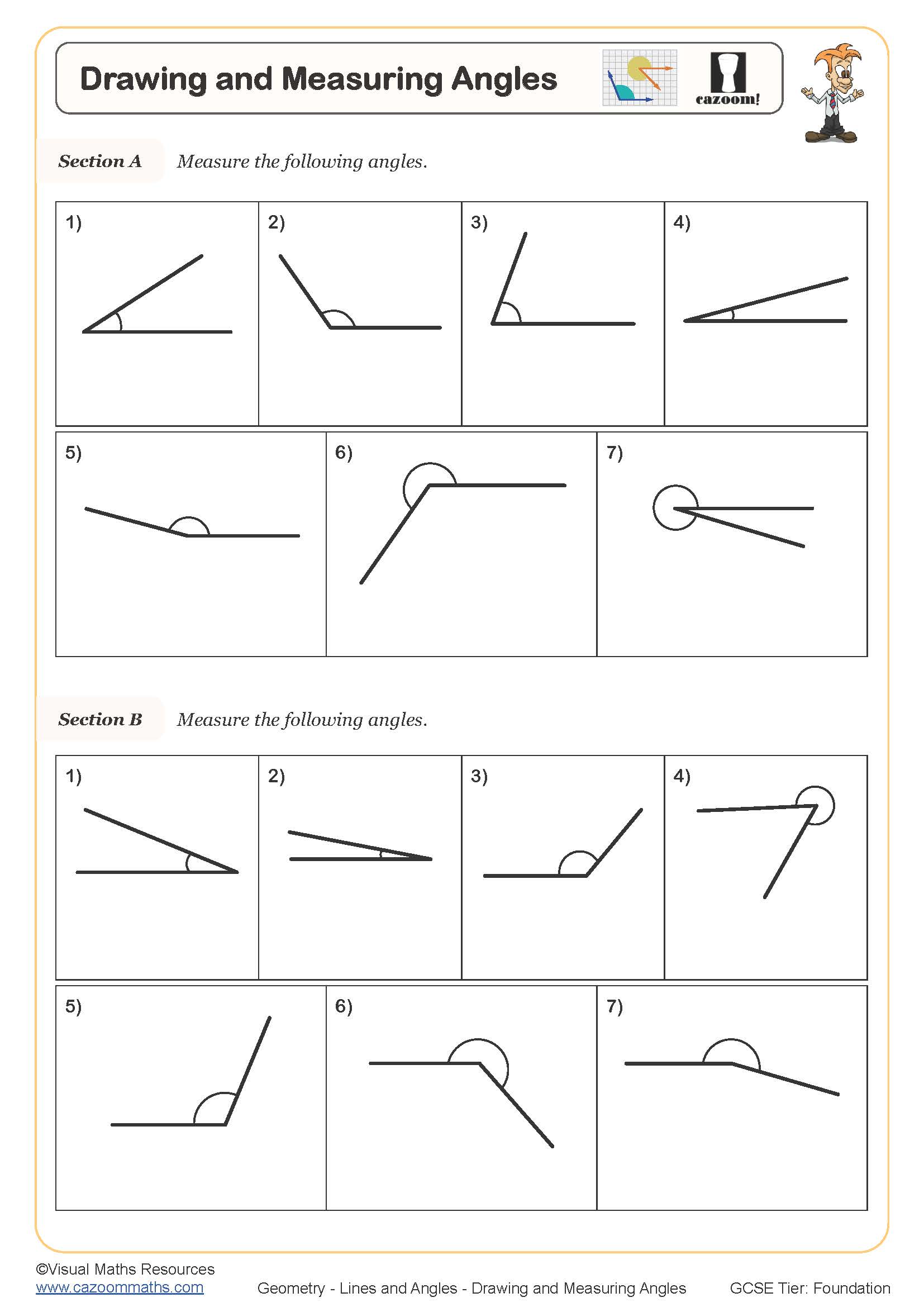
Drawing and Measuring Angles
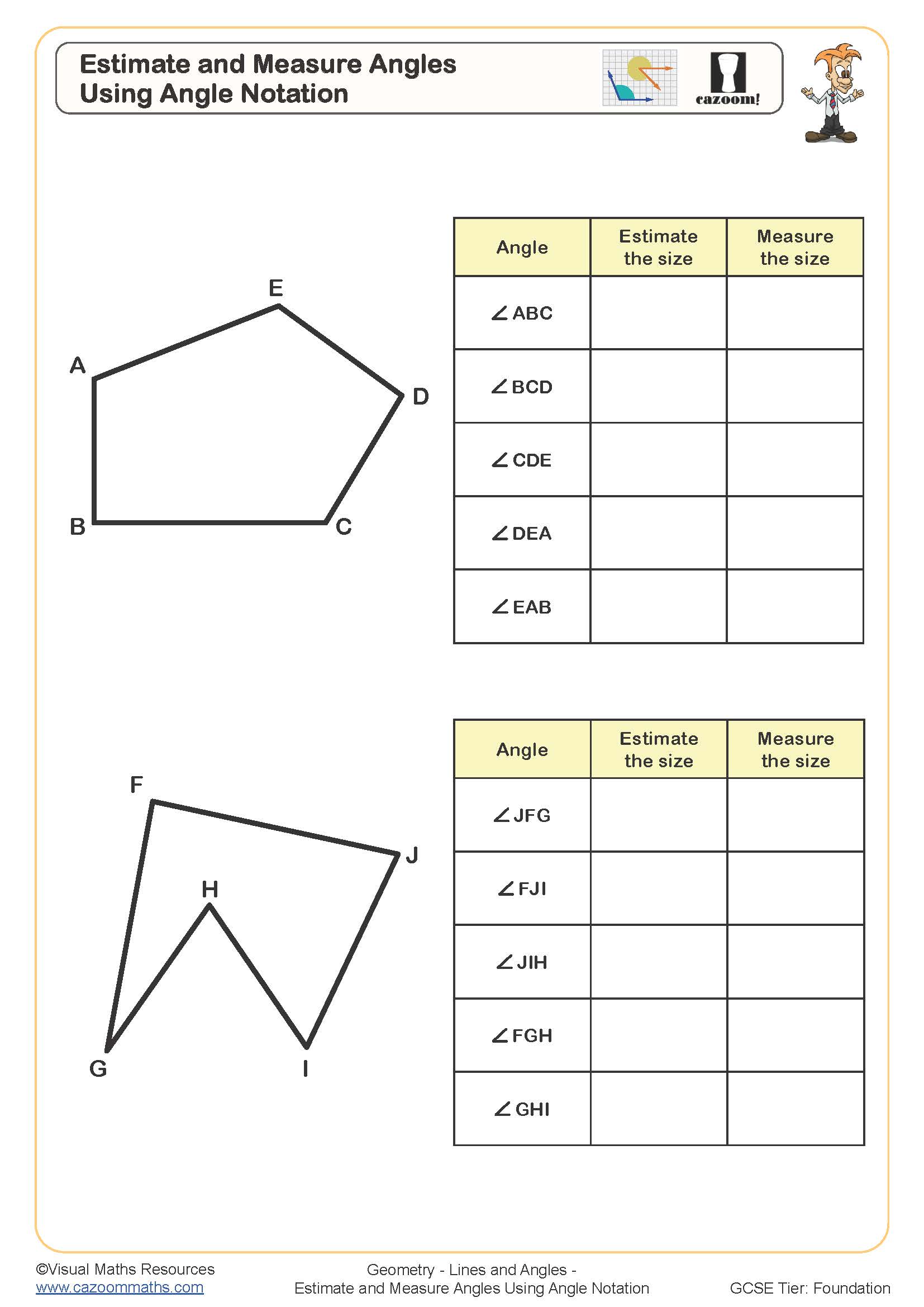
Estimate and Meaure Angles using Angle Notation
Parallel and Perpendicular Lines
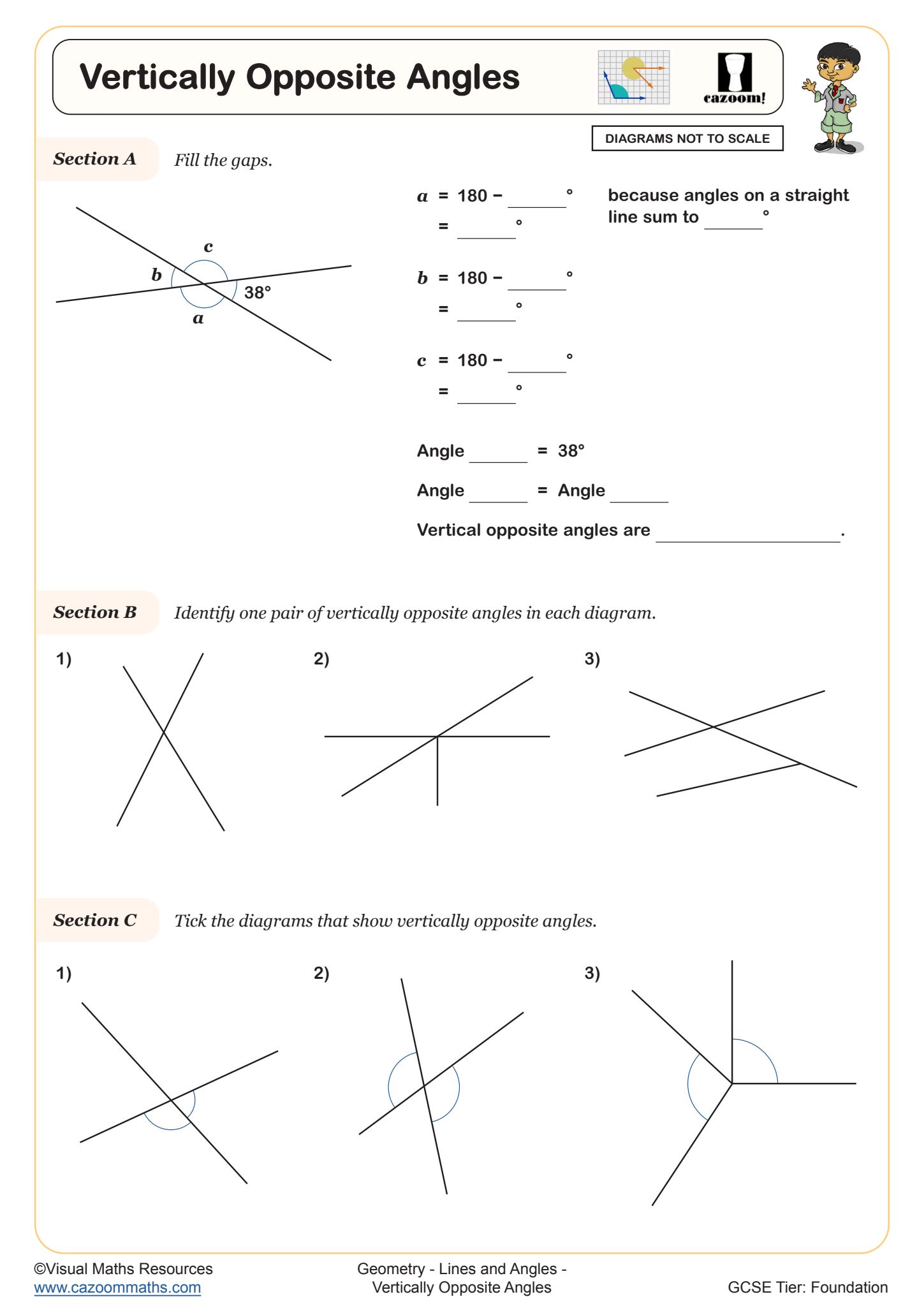
Vertically Opposite Angles
