KS4 Volume and Surface Area Worksheets
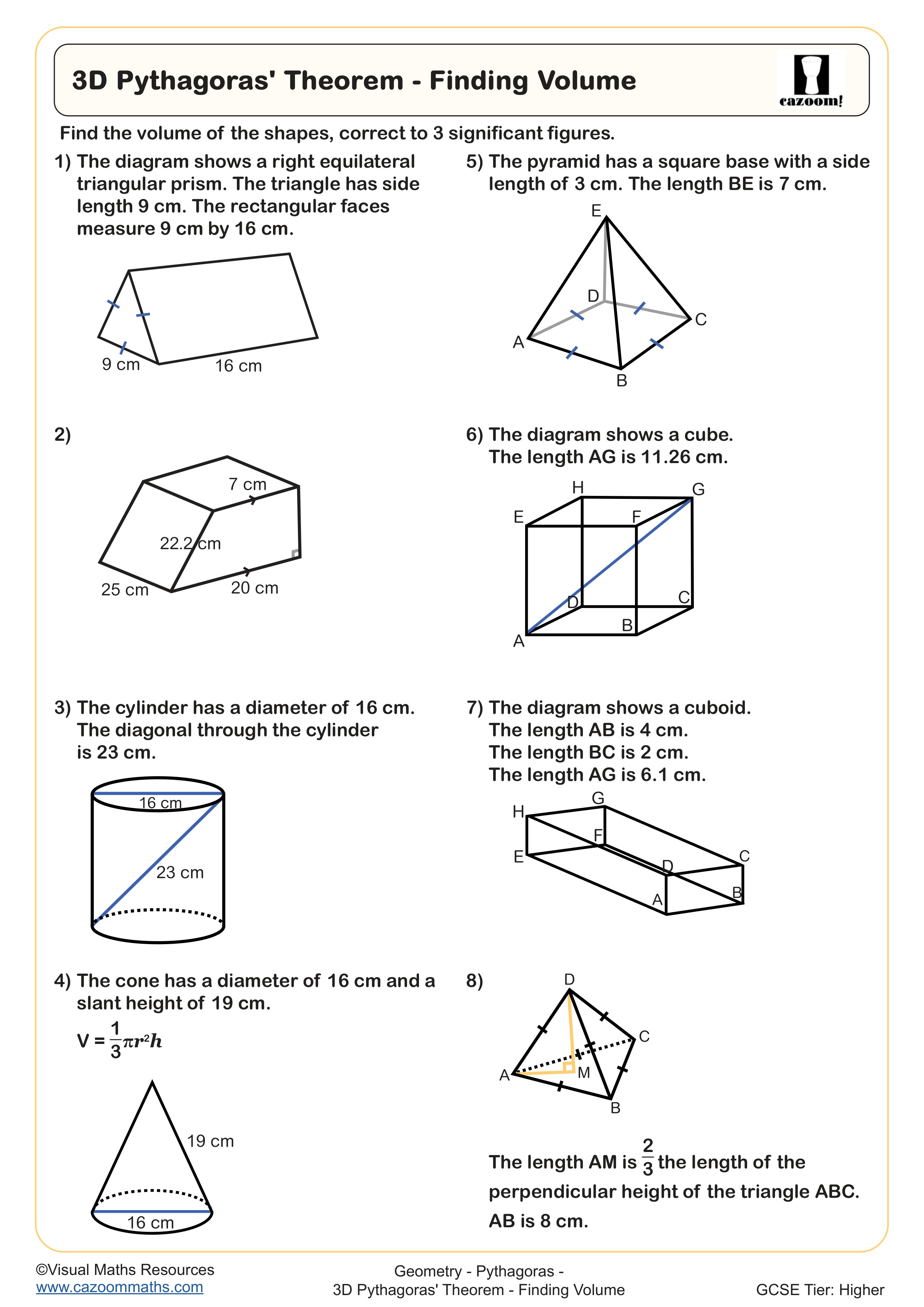
3D Pythagoras' Theorem - Finding Volume
Area and Volume of Similar Shapes (A)

Area and Volume of Similar Shapes (B)

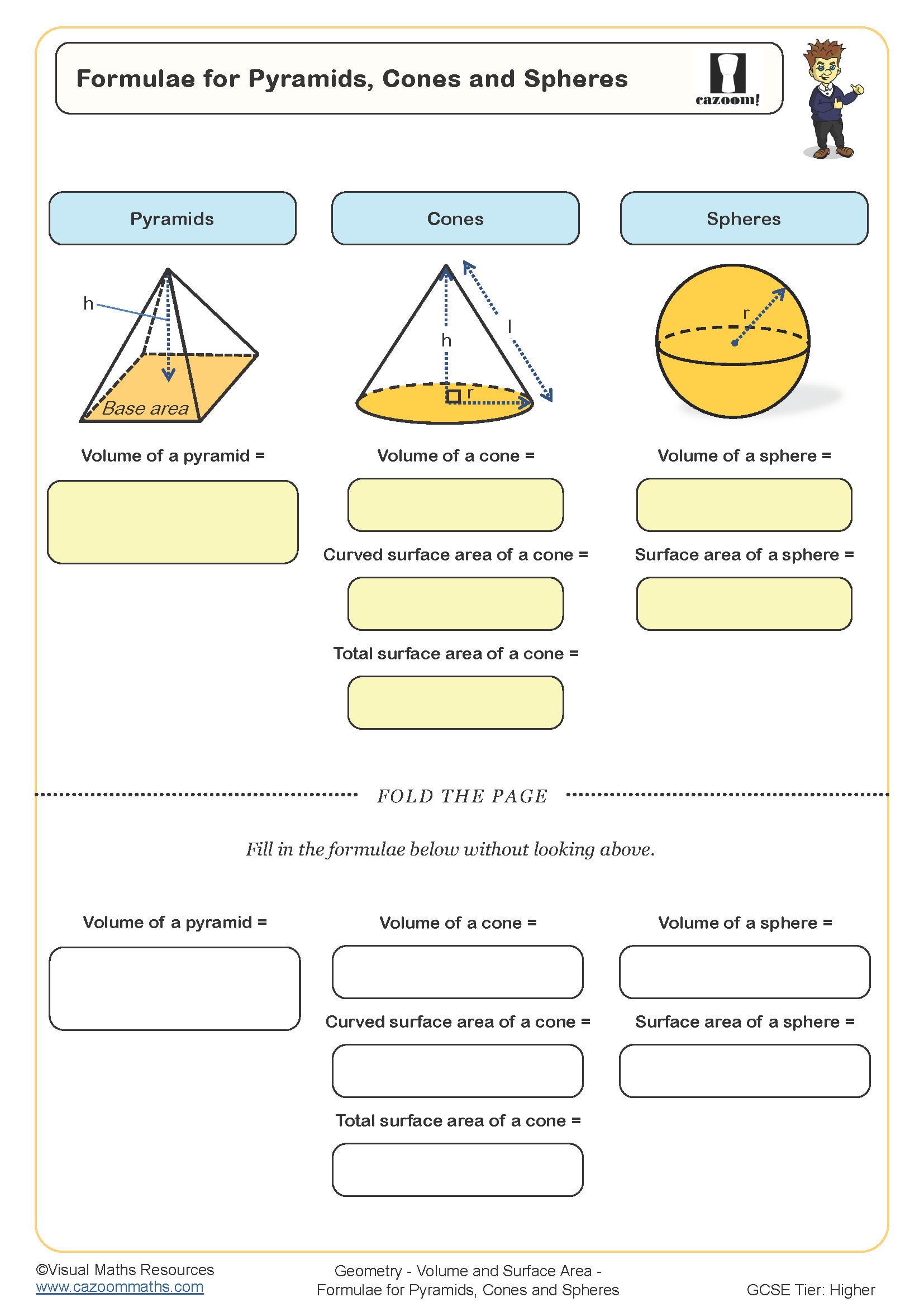
Formulae for Pyramids Cones and Spheres
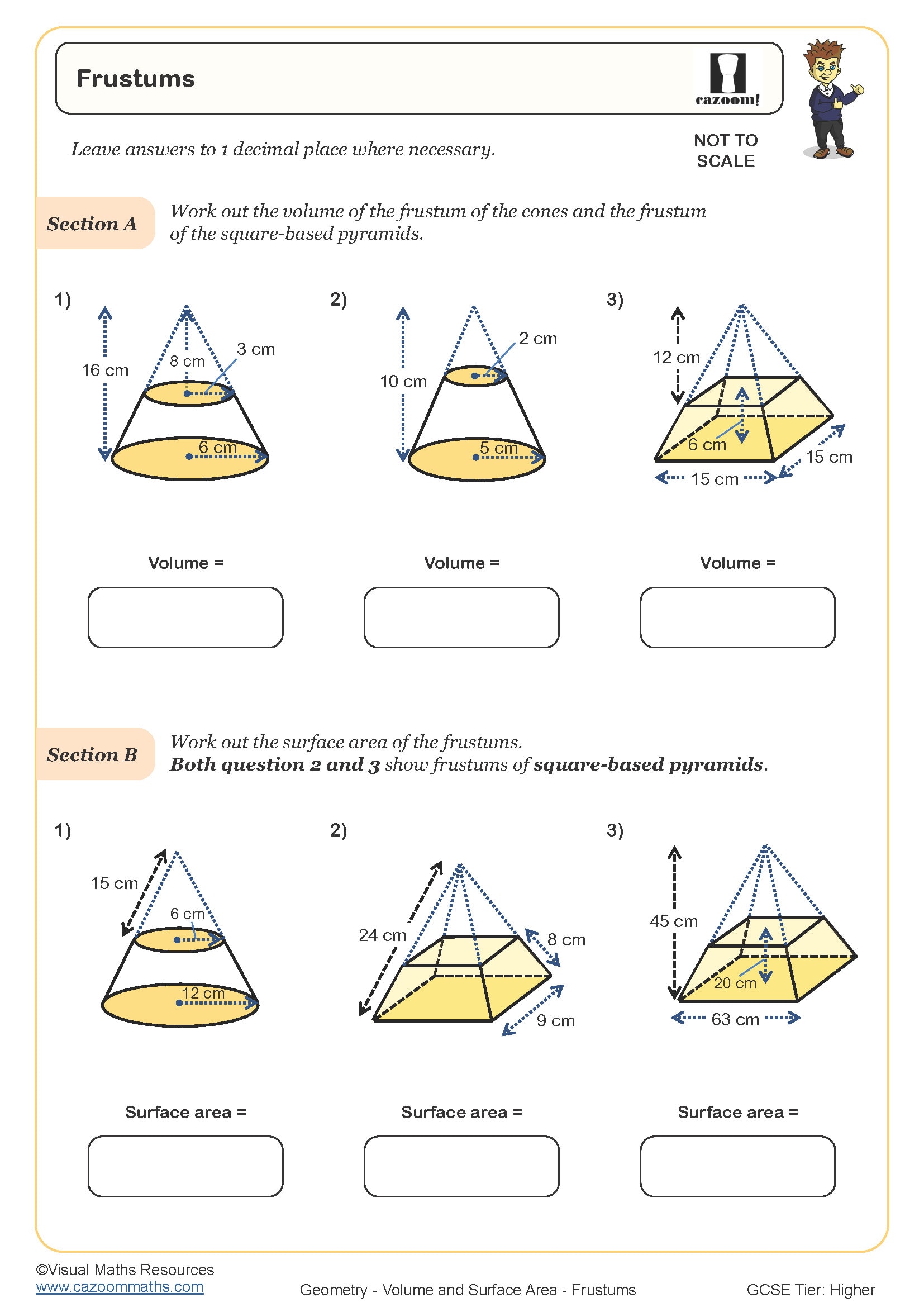
Frustums
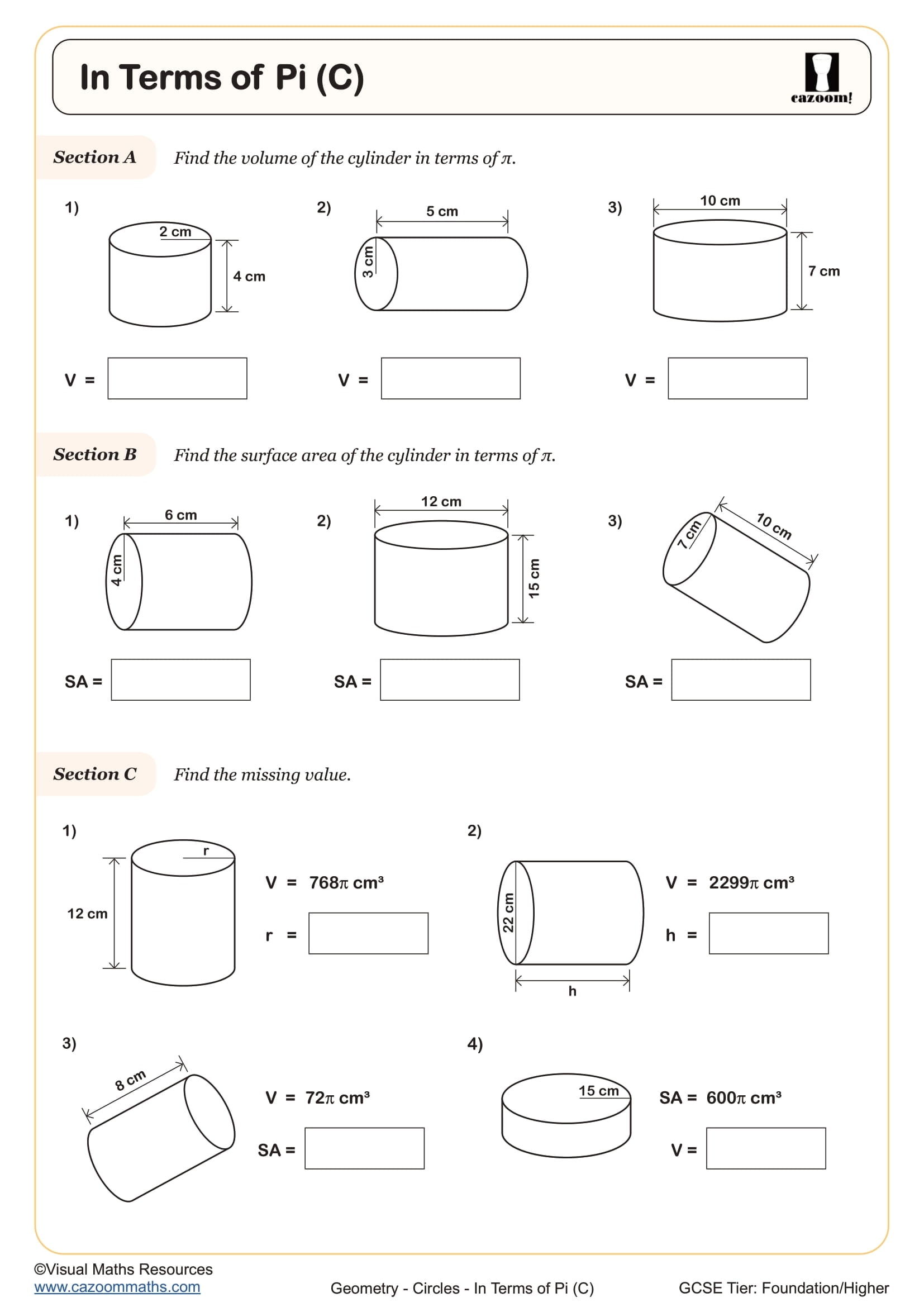
In Terms of Pi (C)
Recognising Prisms
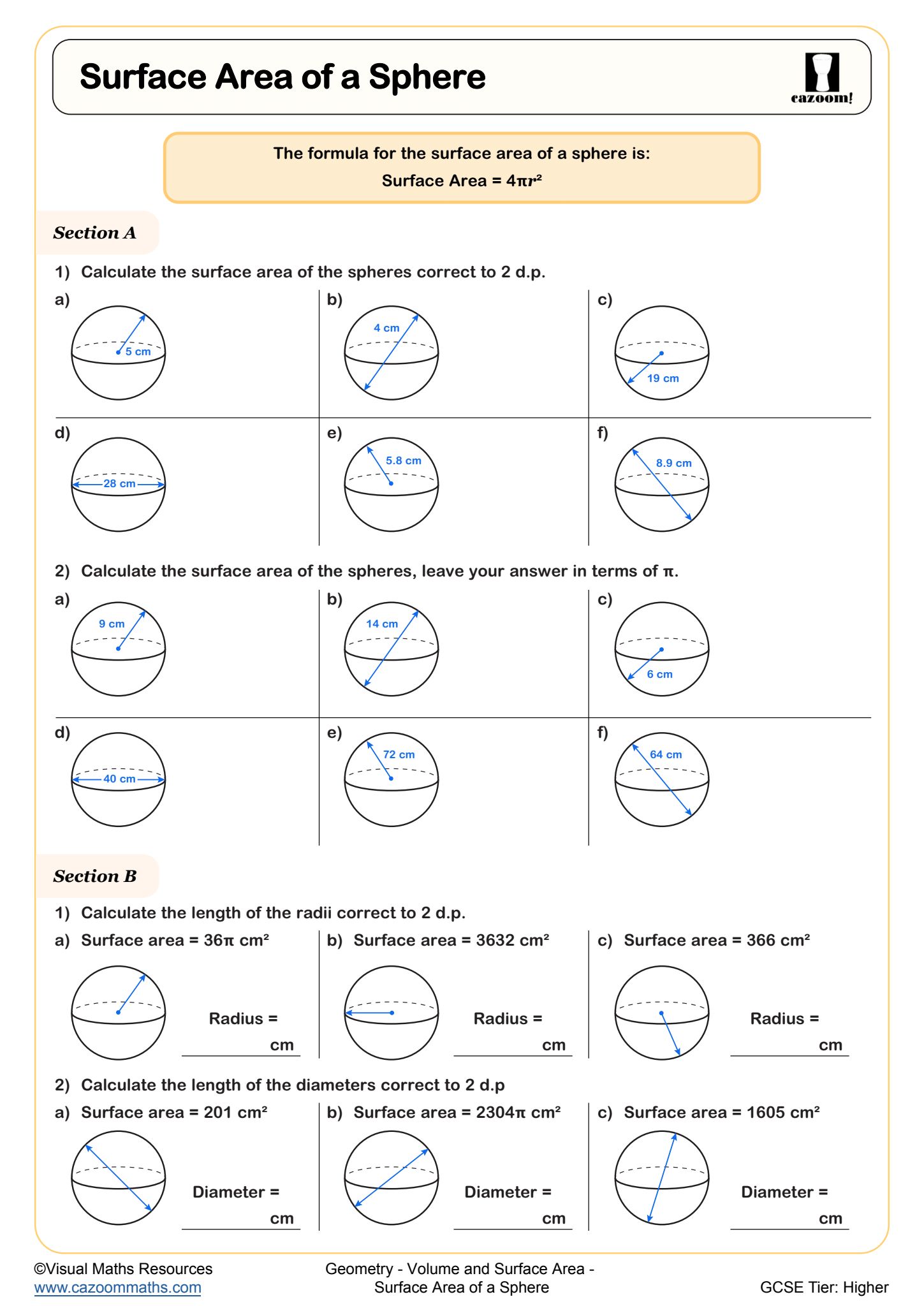
Surface Area of a Sphere
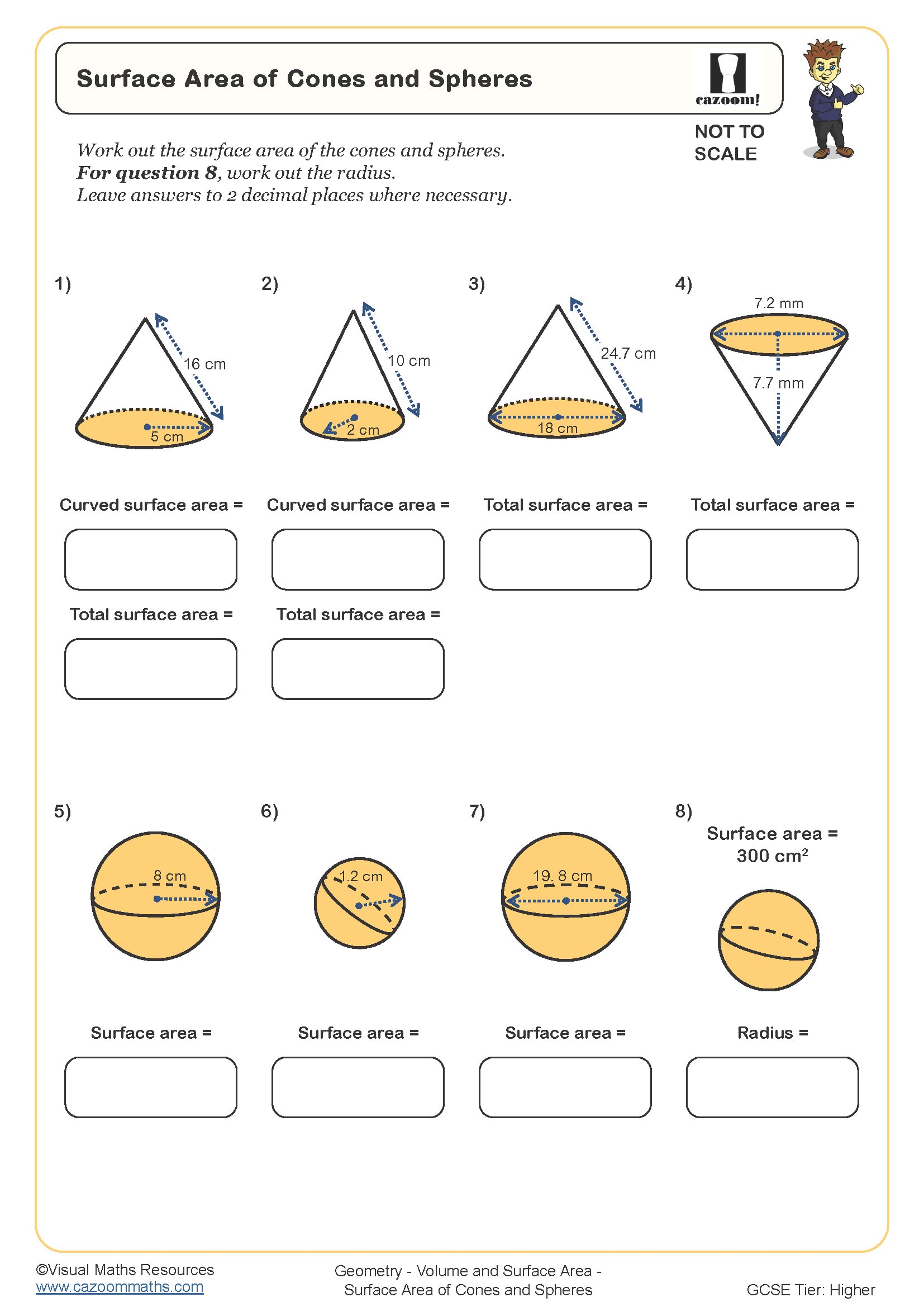
Surface Area of Cones and Spheres
Surface Area of Conical Frustums

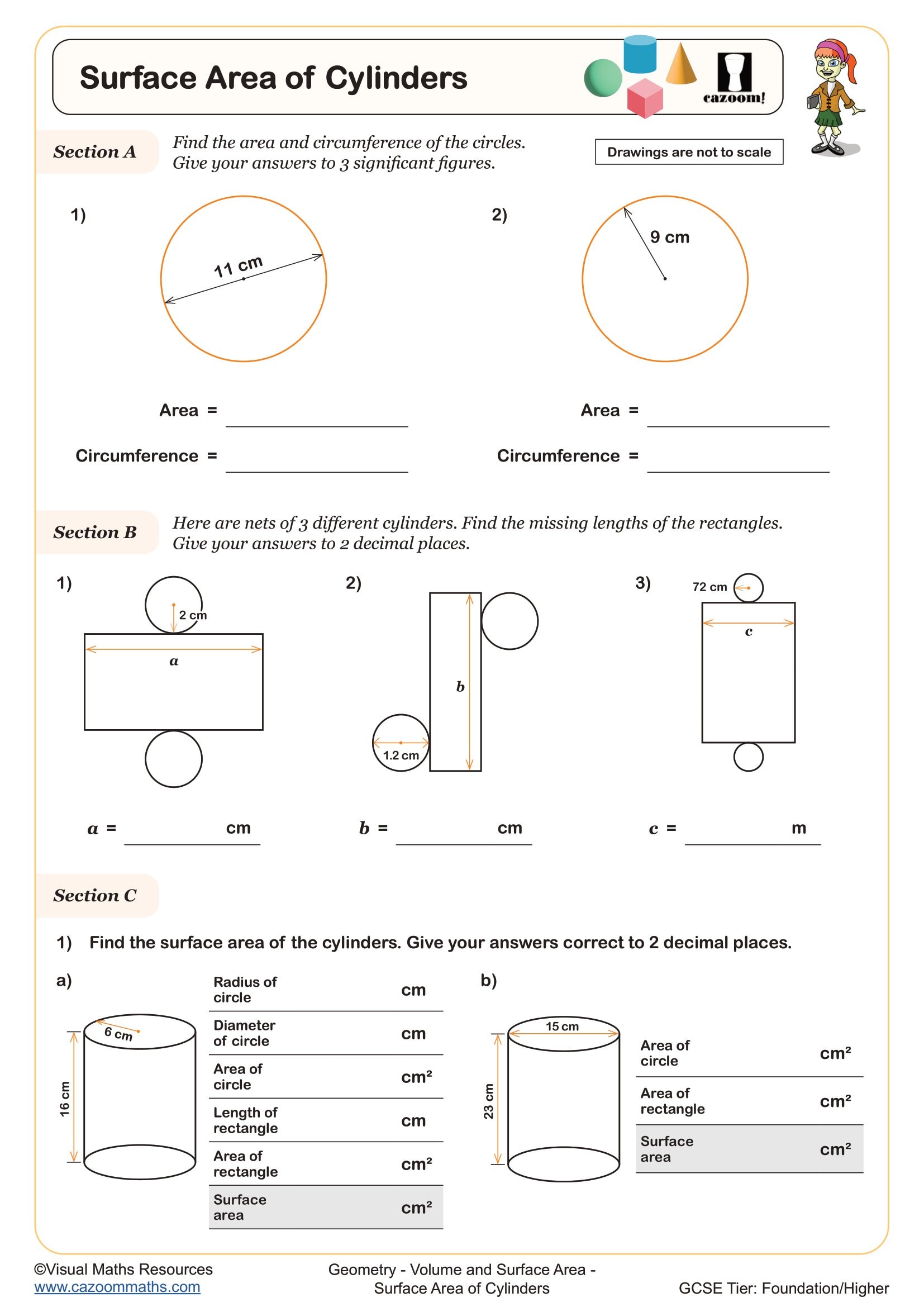
Surface Area of Cylinders
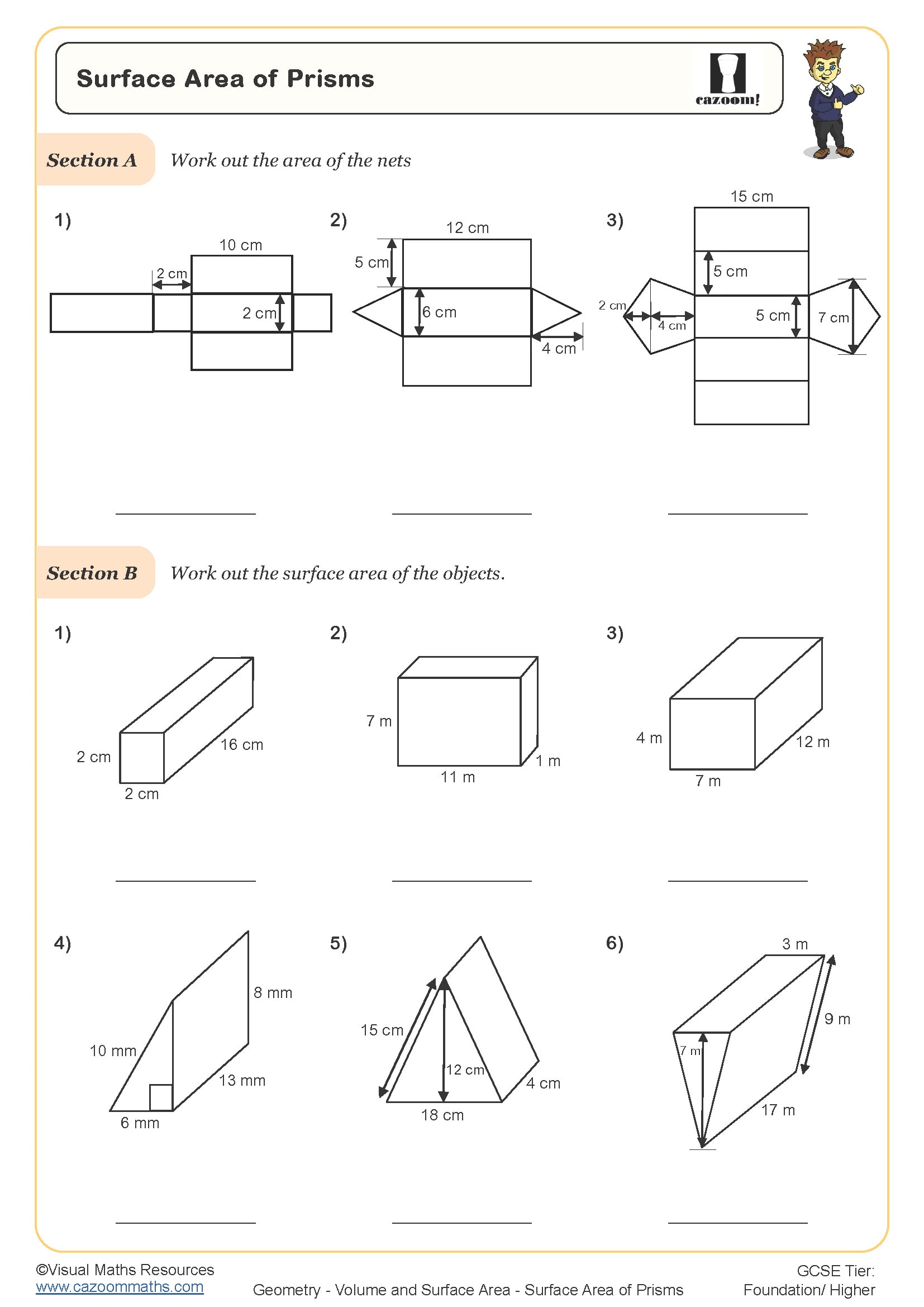
Surface Area of Prisms
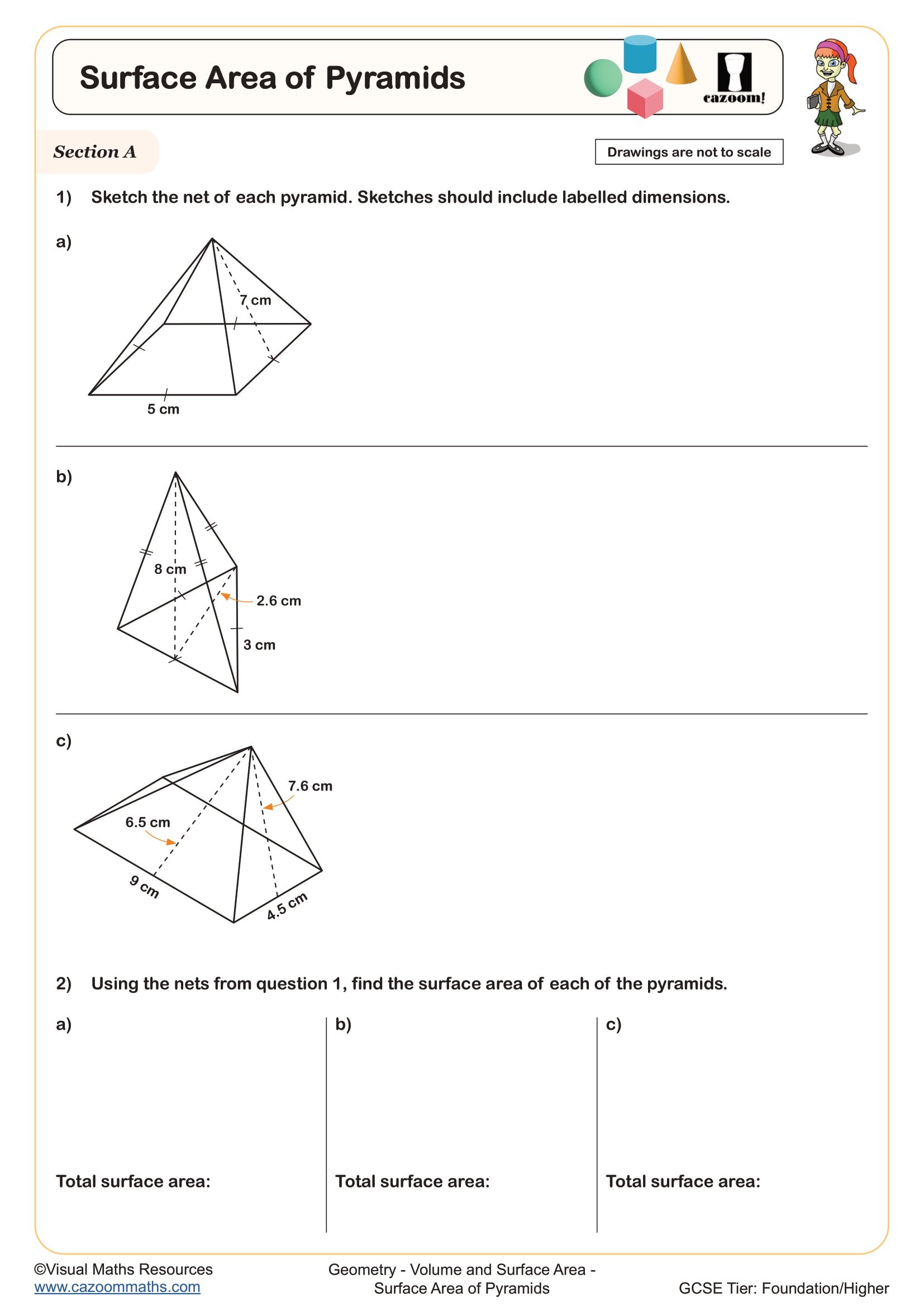
Surface Area of Pyramids
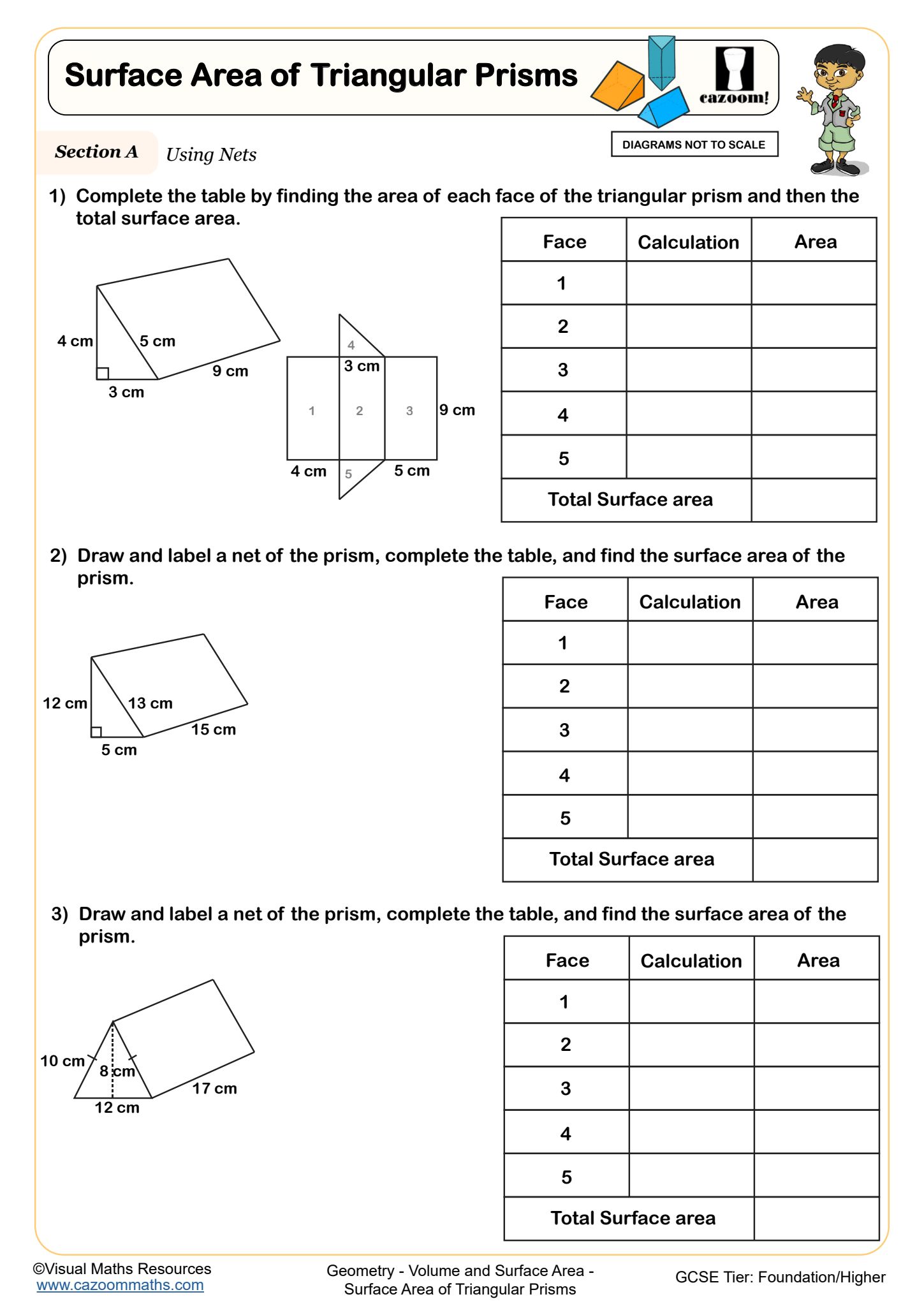
Surface Area of Triangular Prisms
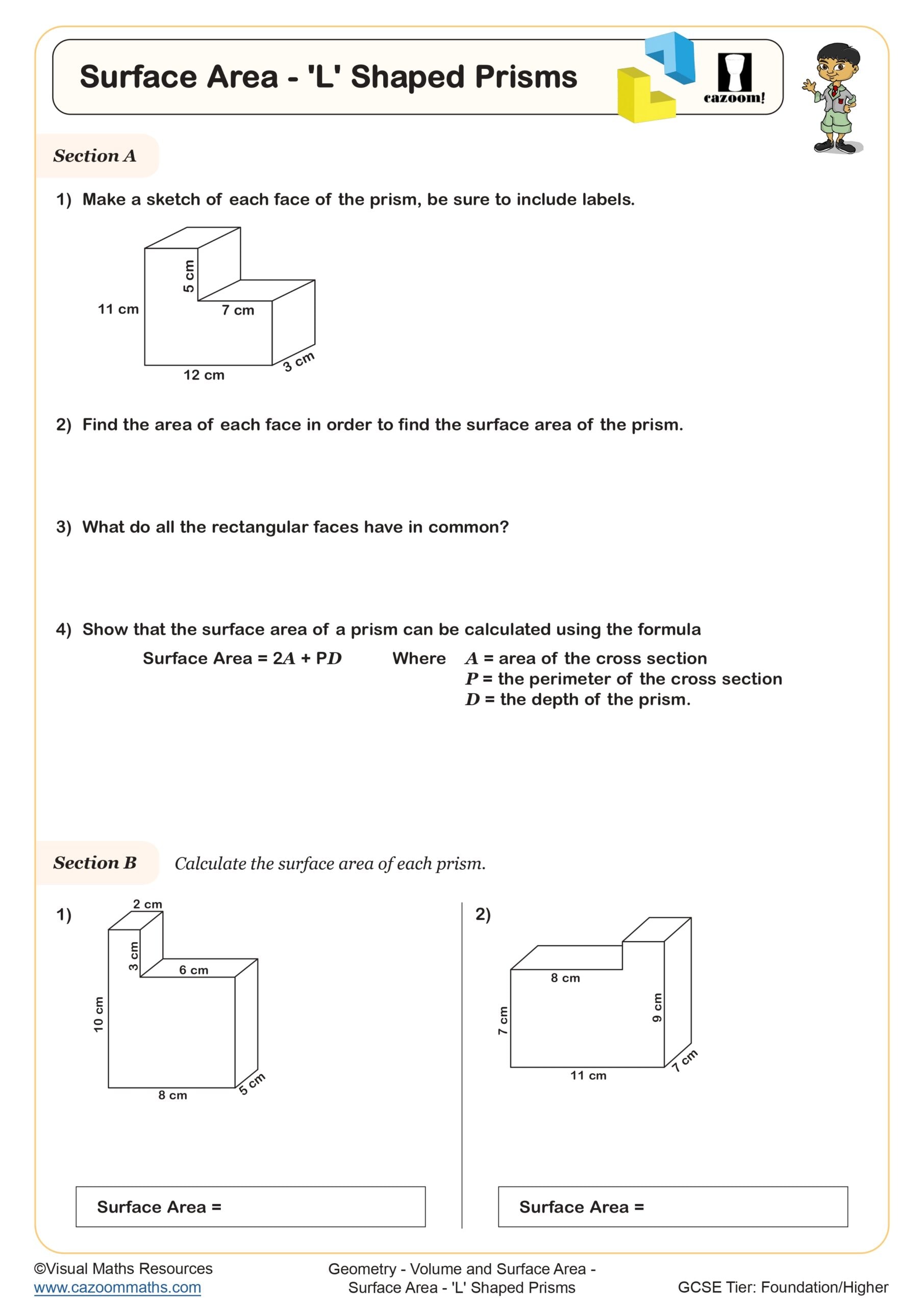
Surface Area- 'L' Shaped Prisms
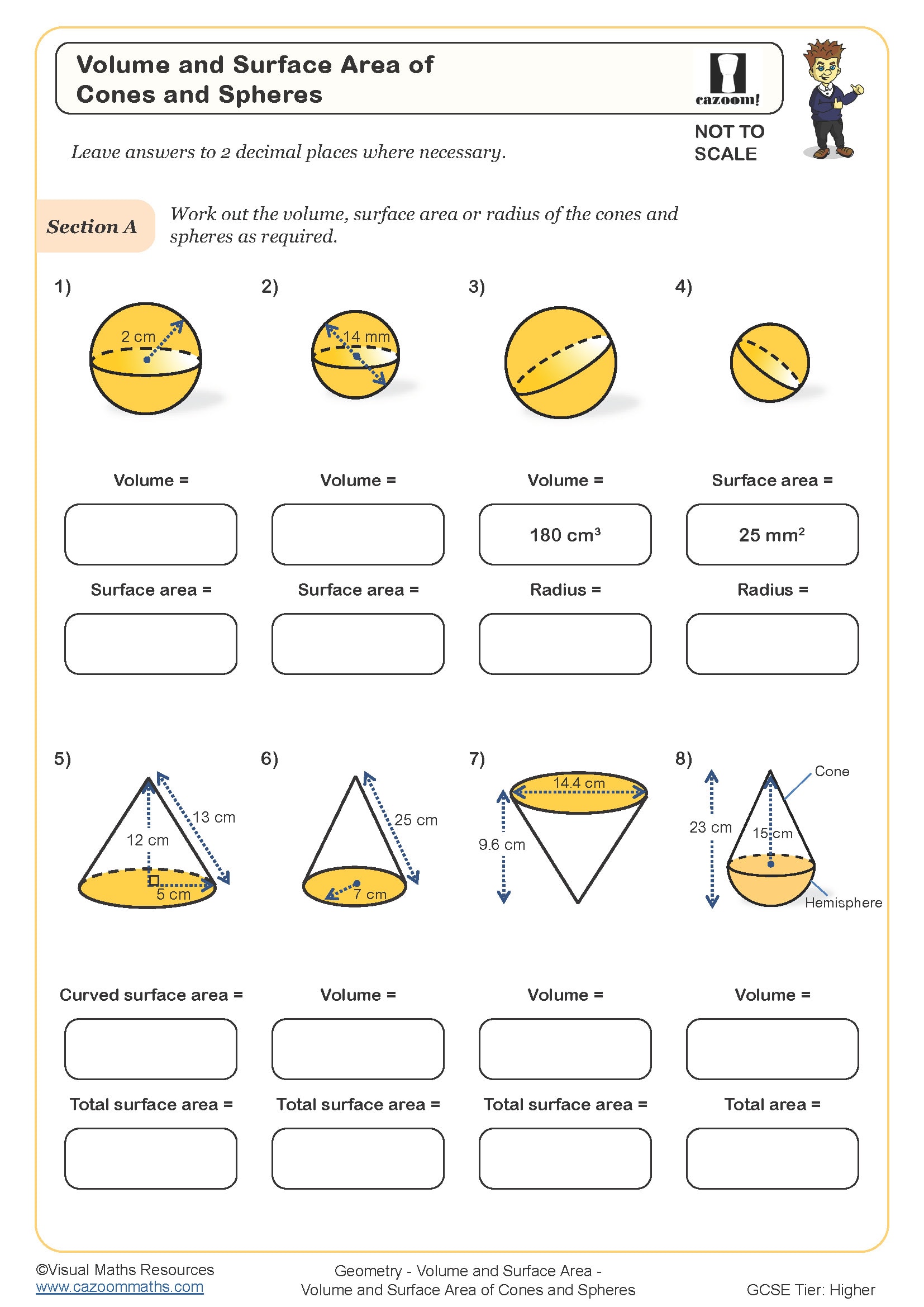
Volume and Surface Area of Cones and Spheres
Volume of a Cone

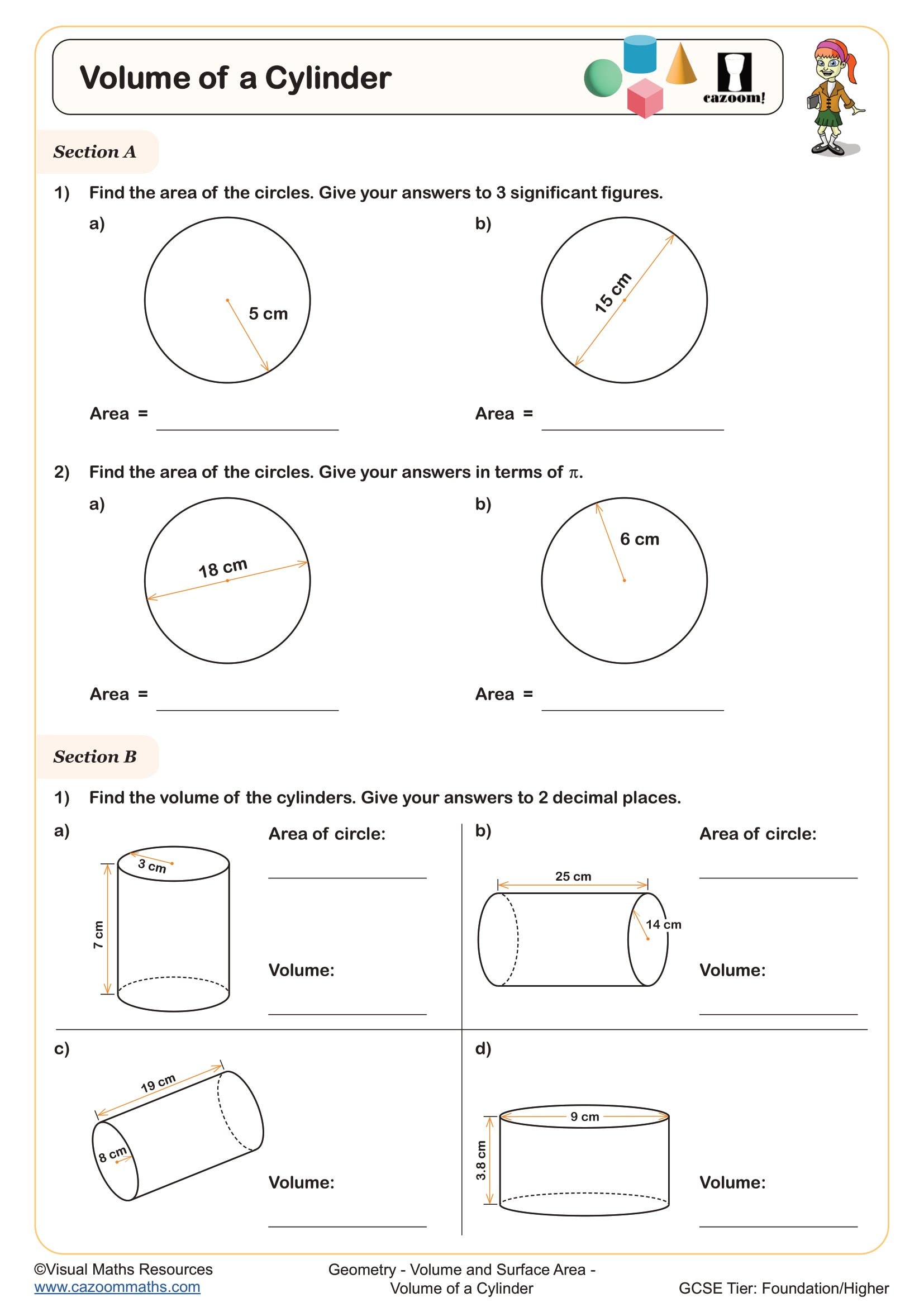
Volume of a Cylinder
Volume of a Pyramid

Volume of a Sphere

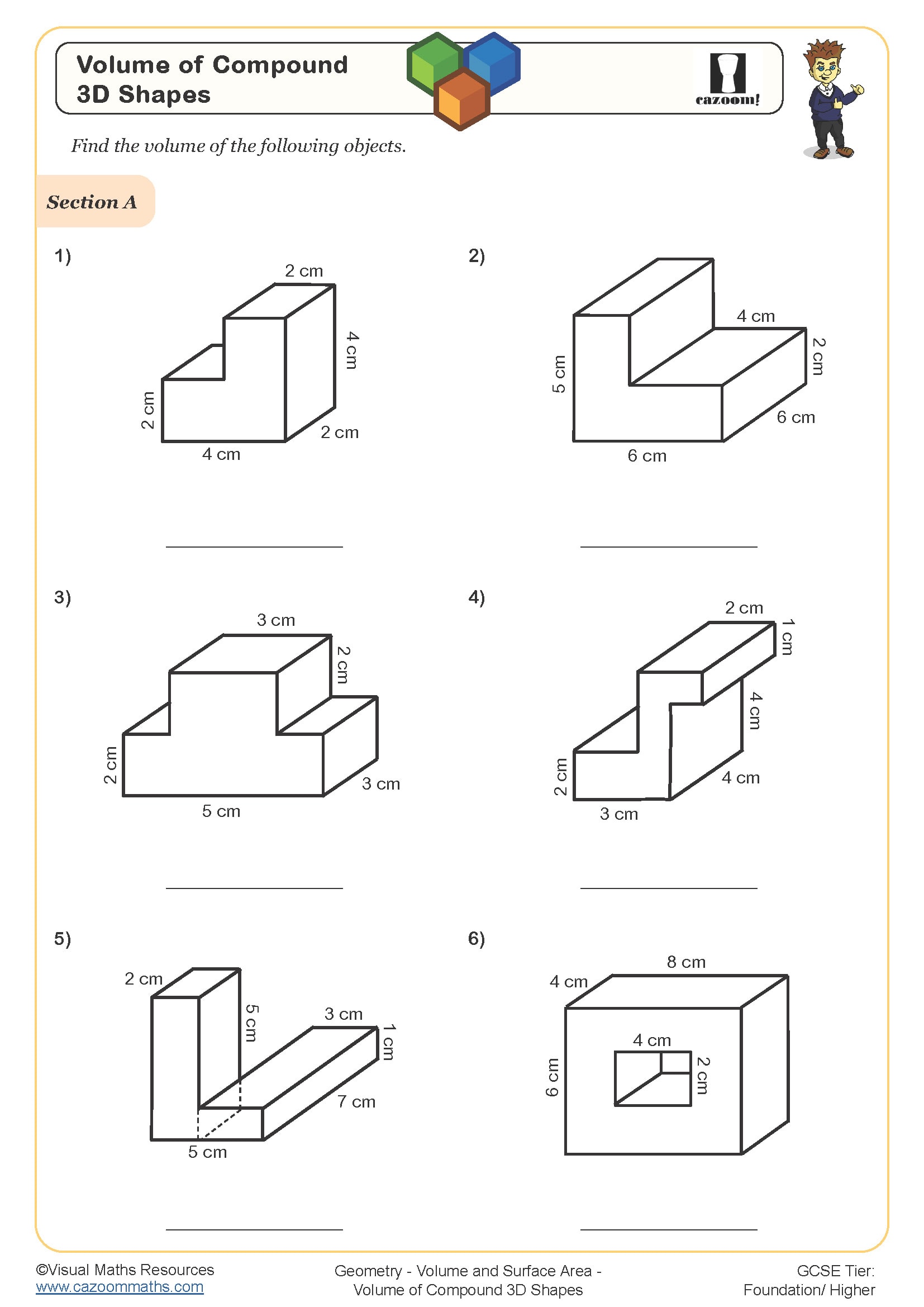
Volume of Compound 3D shapes
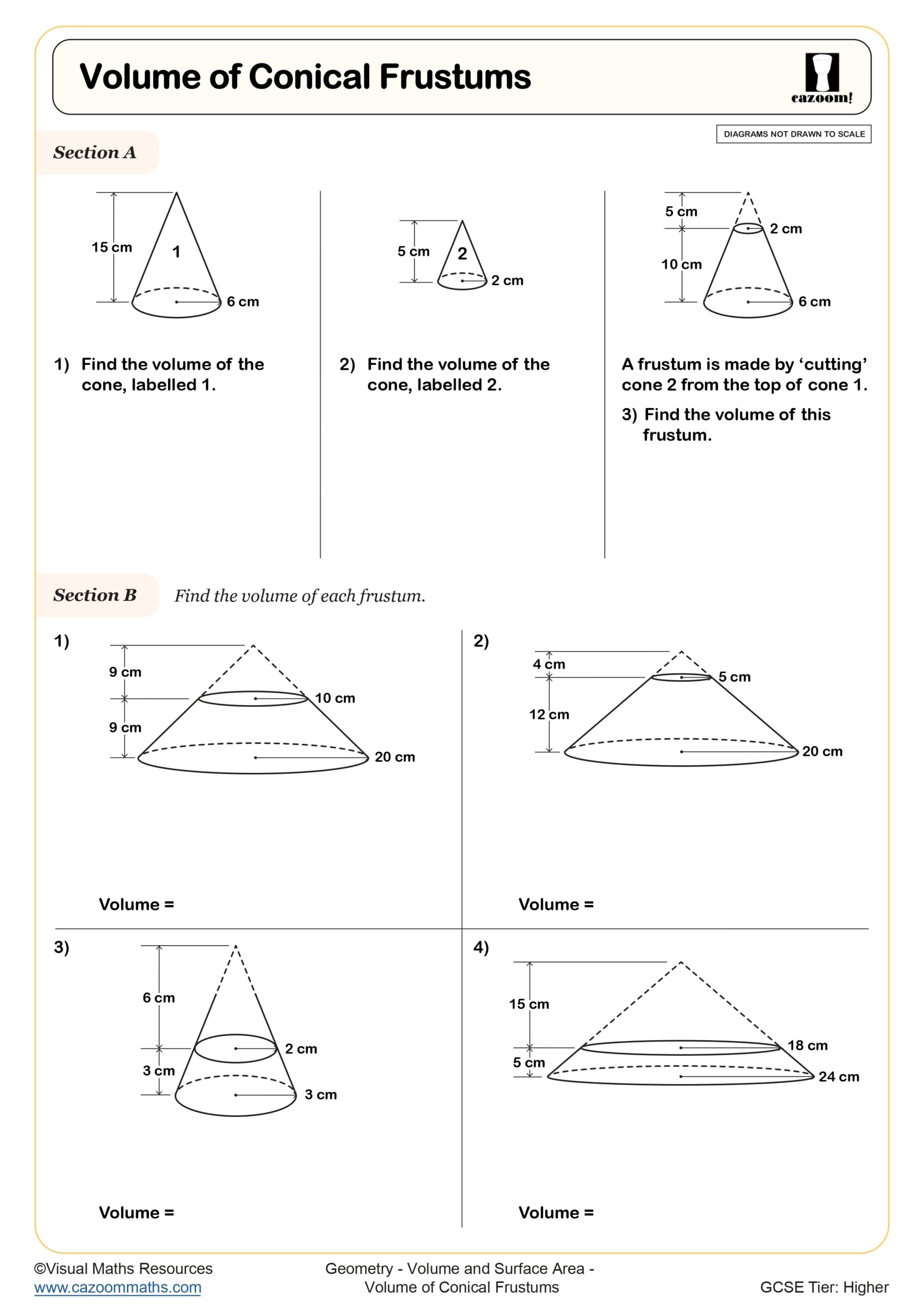
Volume of Conical Frustums
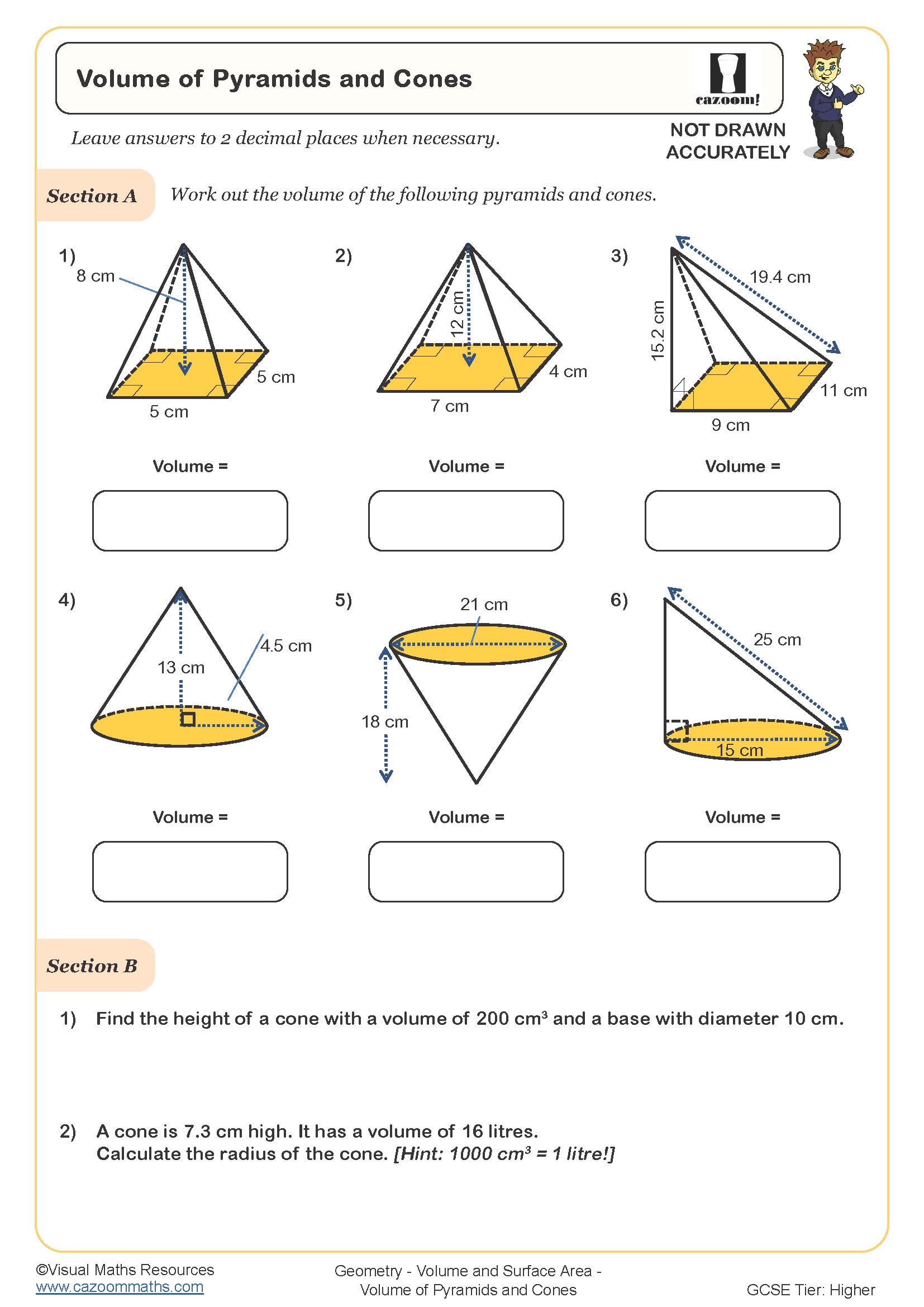
Volume of Pyramids and Cones
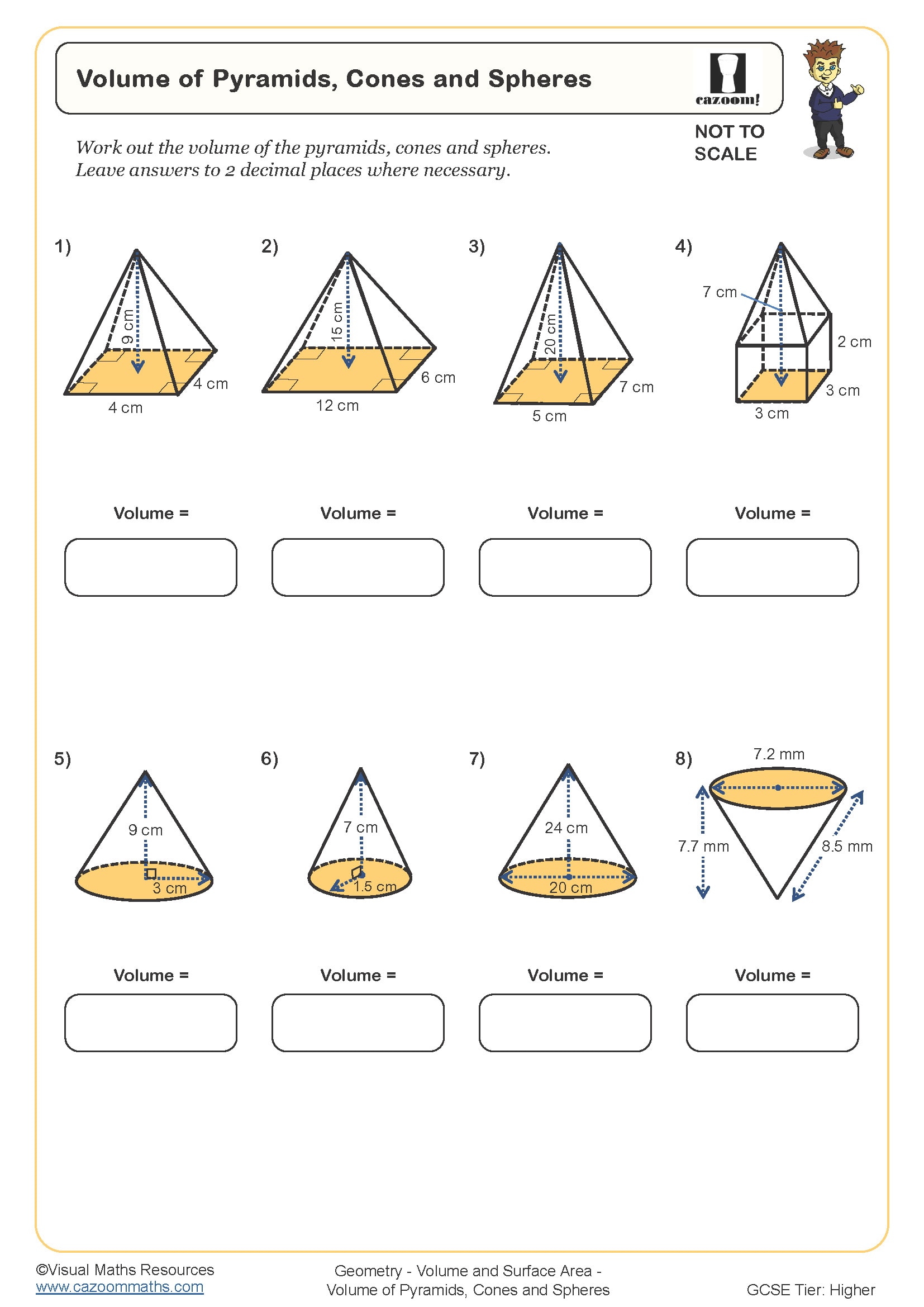
Volume of Pyramids Cones and Spheres
Volume of Square-based Pyramid Frustums

Volume Word Problems

What is the difference between volume and surface area?
Volume measures the three-dimensional space inside a shape (cubic units such as cm³ or m³), while surface area measures the total area of all outer faces (square units such as cm² or m²). At GCSE level, students must select appropriate formulae and units based on what the question asks, which appears regularly on both Foundation and Higher tier papers.
A common error occurs when students apply volume formulae to surface area questions, or vice versa. Teachers often observe students calculating the area of one face correctly but forgetting to multiply by the number of identical faces on prisms, or including bases that should be excluded in open-topped containers. Exam mark schemes penalise unit errors heavily, so students need consistent practice identifying which measurement applies to each context.
Which year groups study volume and surface area?
These worksheets target Year 10 and Year 11 students following the KS4 curriculum. Volume and surface area of standard prisms typically appears early in Year 10, with pyramids, cones, and spheres introduced as students progress towards higher tier GCSE content. The topic builds on the area and perimeter work from KS3, now extended into three dimensions with more sophisticated shapes.
Progression across KS4 involves moving from straightforward prisms with given dimensions to problems requiring multiple steps: finding missing lengths first, working with compound shapes, or converting units before calculation. By Year 11, students tackle examination-style questions that combine volume and surface area with ratio, density, or real-world contexts where they must interpret which calculation the scenario requires.
How do you calculate the surface area of a pyramid?
The surface area of a pyramid combines the base area with the areas of the triangular faces. For a square-based pyramid, calculate the area of the square base, then find the area of each triangular face using ½ × base × slant height, and sum all components. Students must distinguish between the perpendicular height (used for volume) and the slant height (used for surface area of faces), which often causes confusion in examinations.
This calculation appears in packaging design and construction, where material costs depend on surface area rather than volume. Architects calculating roof coverings for pyramid-topped buildings, or engineers determining the amount of protective coating needed for pyramidal structures, rely on accurate surface area calculations. The Egyptian pyramids at Giza required precise surface area estimates to determine the limestone casing needed, connecting this mathematical concept to one of history's most remarkable engineering achievements.
How do these worksheets help students master volume and surface area?
The worksheets provide structured practice with each shape type, starting with clear formulae and moving through worked examples before students attempt independent questions. Answer sheets allow students to check their working immediately, identifying where errors occur in their method rather than just getting a final answer wrong. This self-correction process helps students recognise whether they've selected the wrong formula, made calculation errors, or misread units.
Teachers use these resources effectively for differentiated homework, setting specific sections to groups based on their confidence with particular shapes. They work well for intervention sessions where students need focused practice on pyramids or spheres after initial teaching. Many teachers find them valuable for pre-exam revision, allowing students to identify gaps in their knowledge across all shape types, then concentrate effort on weaker areas with targeted practice questions.