KS3 Equivalent Fractions Worksheets
Equivalent Fractions (A)

Equivalent Fractions (B)

Equivalent Fractions (C)
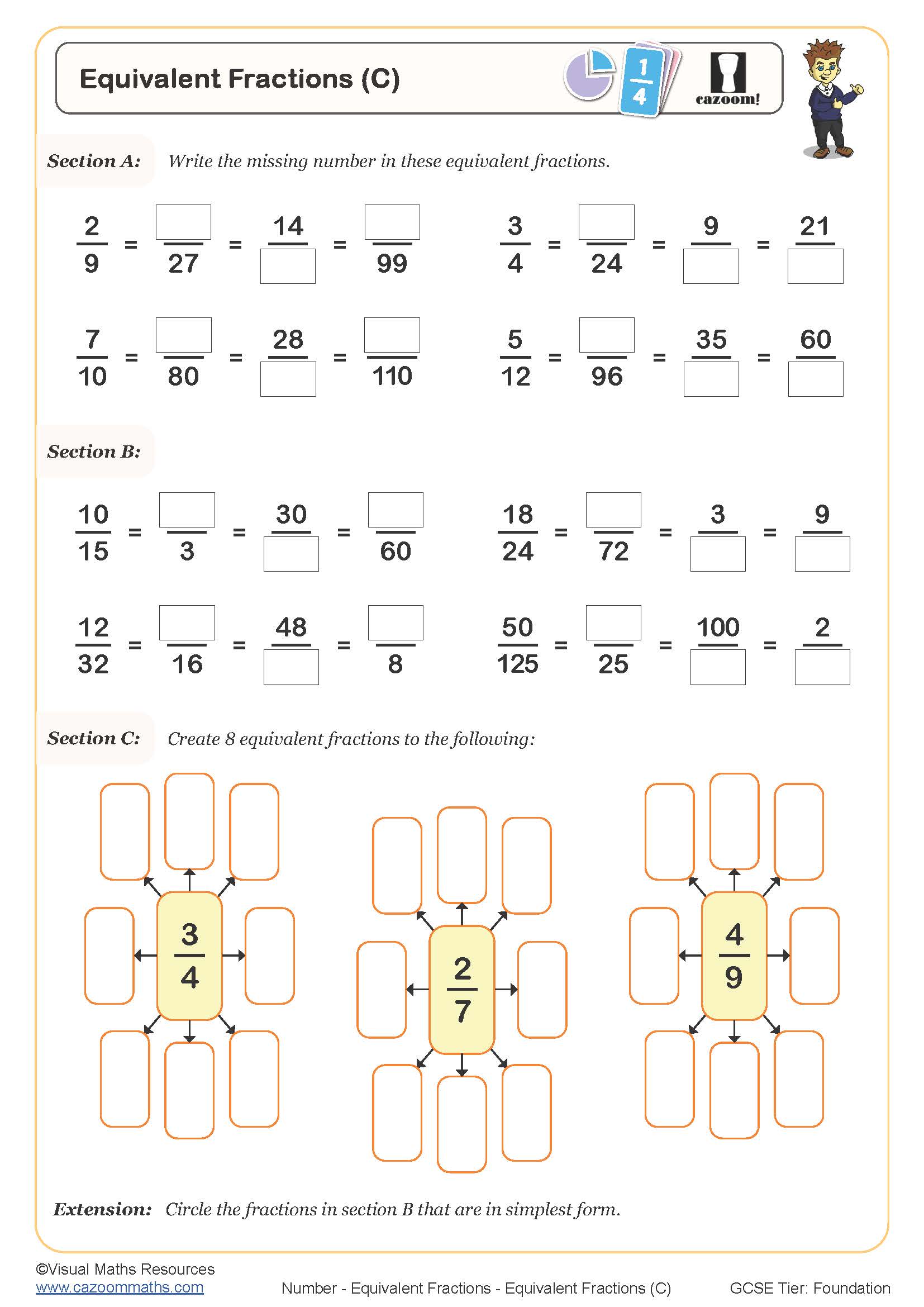
Fractions Equivalent to One Half
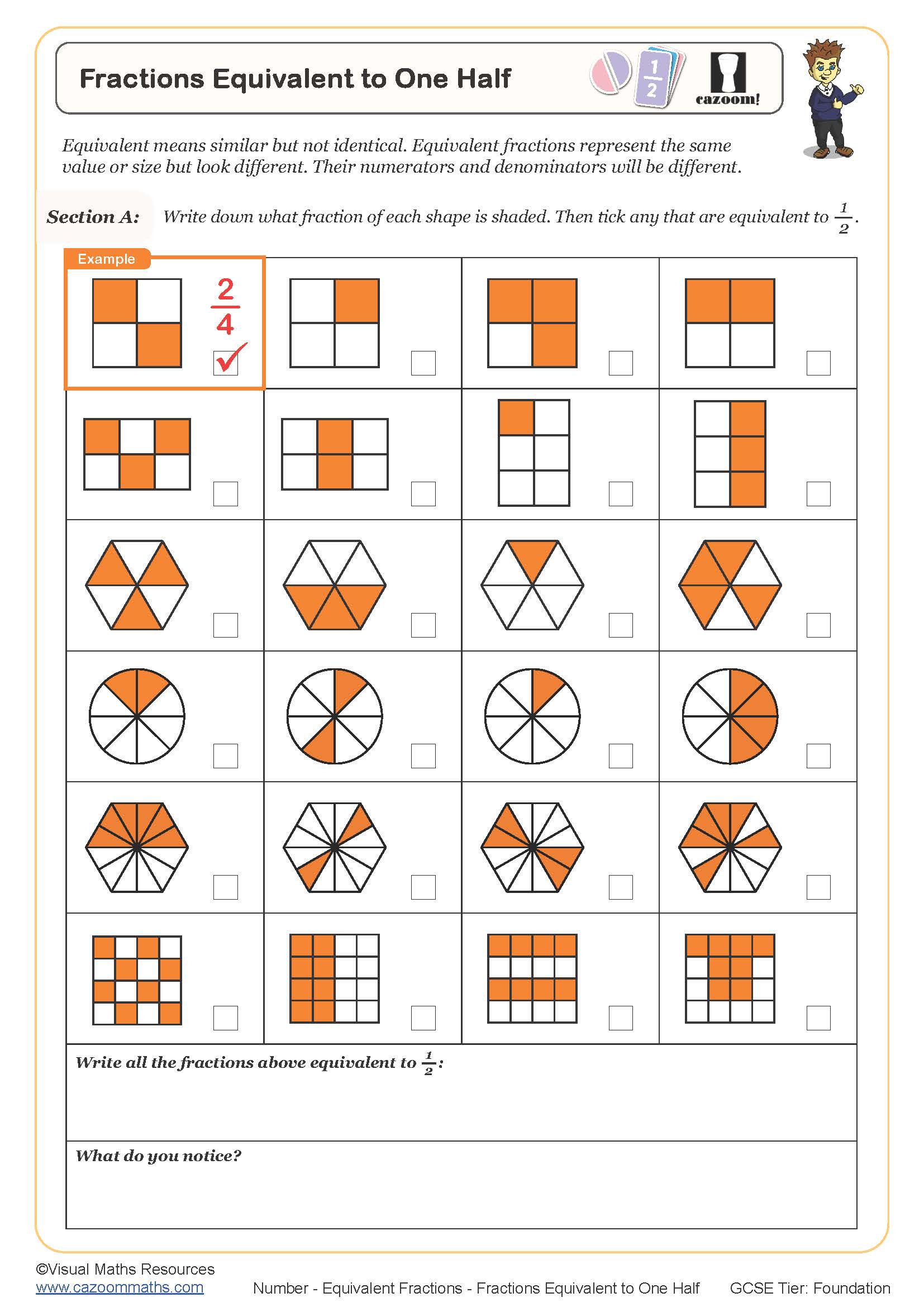
Fractions Equivalent to One Quarter
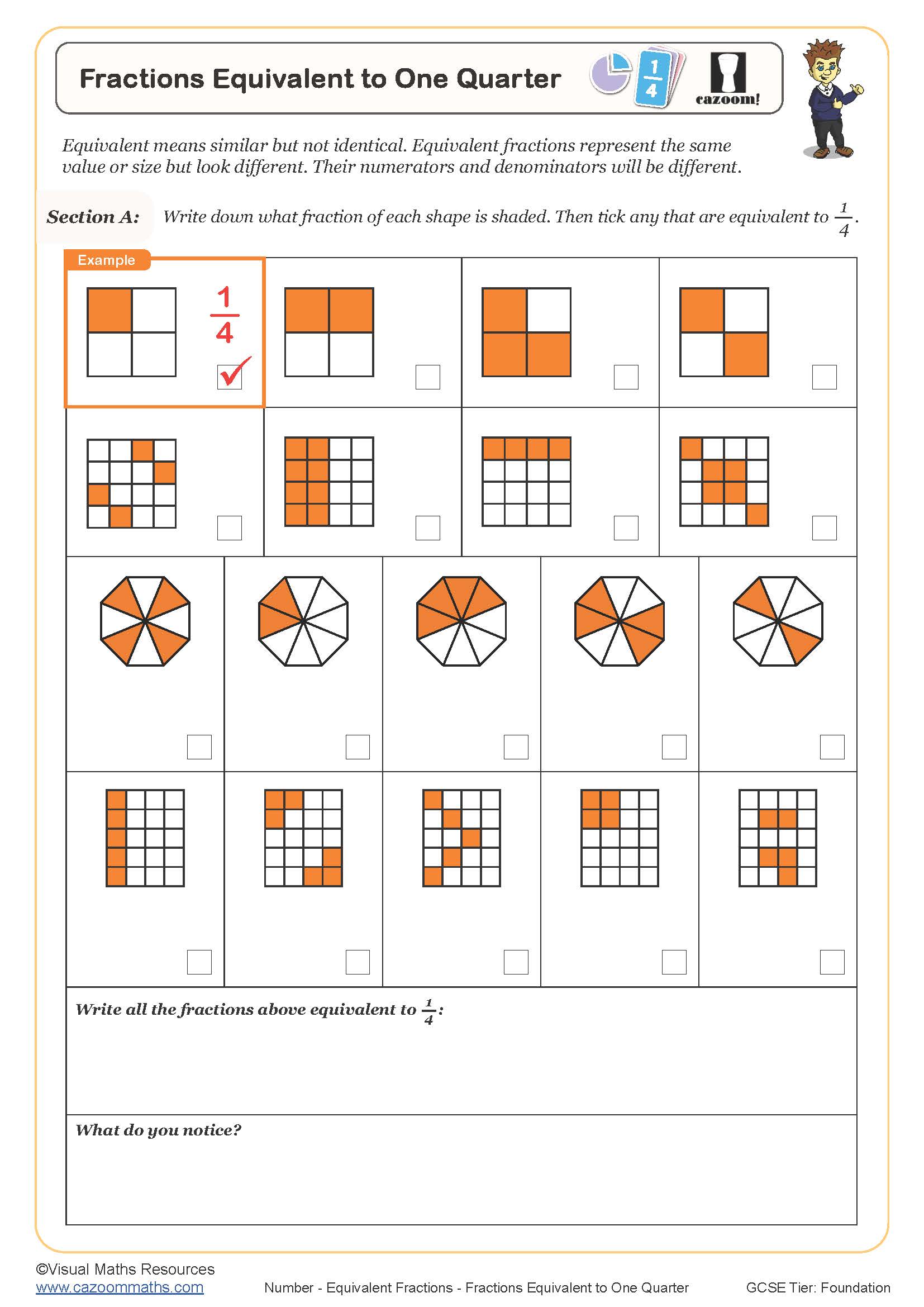
Fractions Equivalent to One Third
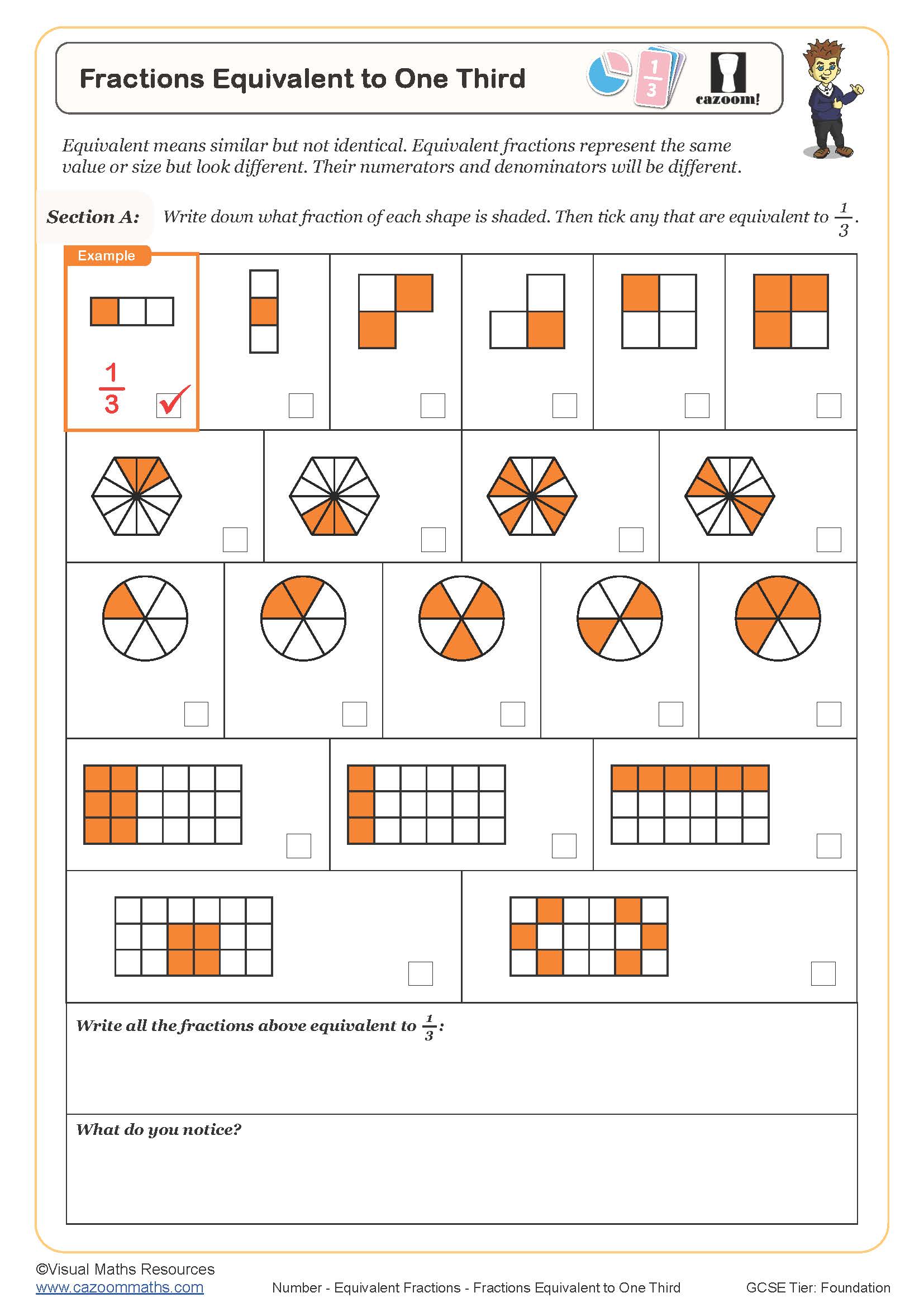
Identifying Equivalent Fractions

Introducing the Fraction Wall

Manipulating Fractions

Using The Fraction Wall - Equivalent Fractions

What Are Equivalent Fractions and Why Do Students Need to Learn Them?
Equivalent fractions are fractions that represent the same proportion or value but use different numerators and denominators, such as ½, 2/4, and 3/6. The National Curriculum introduces this concept in upper Key Stage 2, but it remains central to KS3 as students apply it to fraction operations, ratio, and algebra. Understanding equivalence allows students to compare fractions, add fractions with different denominators, and simplify expressions throughout secondary maths.
A common error teachers encounter is students treating equivalent fractions as separate procedures rather than understanding the underlying principle: multiplying or dividing both parts of a fraction by the same non-zero number preserves its value. Students who memorise rules without grasping this often make mistakes when simplifying or finding common denominators, particularly in Year 9 algebraic fractions where the same logic applies.
Which Year Groups Cover Equivalent Fractions Worksheets?
These worksheets are designed for Year 7, Year 8, and Year 9 students across Key Stage 3. Year 7 typically revisits equivalent fractions from primary school, securing understanding with systematic multiplication and division of numerator and denominator, alongside visual models like fraction walls. Year 8 work extends to finding missing values in equivalent fraction pairs and connecting equivalence to simplifying fractions to their lowest terms.
By Year 9, students apply equivalent fraction reasoning to more abstract contexts, including algebraic fractions and solving equations involving fractions. The progression moves from concrete fraction families (halves, quarters, eighths) towards working flexibly with any fraction and recognising equivalence as a proportional relationship. This prepares students for GCSE topics where fraction manipulation becomes increasingly sophisticated within algebra and ratio problems.
How Do You Simplify Fractions Using Equivalent Fractions?
Simplifying fractions involves dividing both the numerator and denominator by their highest common factor to create an equivalent fraction in its simplest form. For example, 12/18 simplifies to 2/3 by dividing both parts by 6. Students often simplify in stages (dividing by 2, then 3) rather than finding the HCF immediately, which is mathematically valid but less efficient. Teachers observe that students who understand simplification as creating an equivalent fraction make fewer errors than those who apply it as a disconnected rule.
This skill has direct applications in data handling and probability. When calculating experimental probability, results like 15 successes in 45 trials are meaningless until simplified to 1/3, allowing comparison with theoretical probability. Engineers and architects routinely simplify ratios and scale factors, which are essentially equivalent fractions, when converting between units or creating scaled drawings. Recognising that 150cm:450cm simplifies to 1:3 uses identical reasoning.
How Can Teachers Use These Equivalent Fractions Worksheets in the Classroom?
The worksheets provide structured practice that builds from generating simple equivalent fractions to more complex problems involving simplification and missing numerators or denominators. Each sheet scaffolds difficulty within the same skill set, allowing students to develop confidence before tackling challenging questions. The answer sheets enable students to self-check their work, which supports independent learning and helps them identify specific errors in their reasoning rather than simply marking answers right or wrong.
Teachers frequently use these worksheets for differentiated intervention, assigning specific sheets to students who need consolidation after whole-class teaching. They work effectively as starter activities to activate prior knowledge before lessons on adding fractions or as homework to reinforce classroom learning. Many teachers find them valuable for paired work, where students complete alternate questions then explain their methods to each other, which surfaces misconceptions about why equivalent fractions have equal value despite looking different.