KS3 Substitution Worksheets
Substituting into Expressions (A)
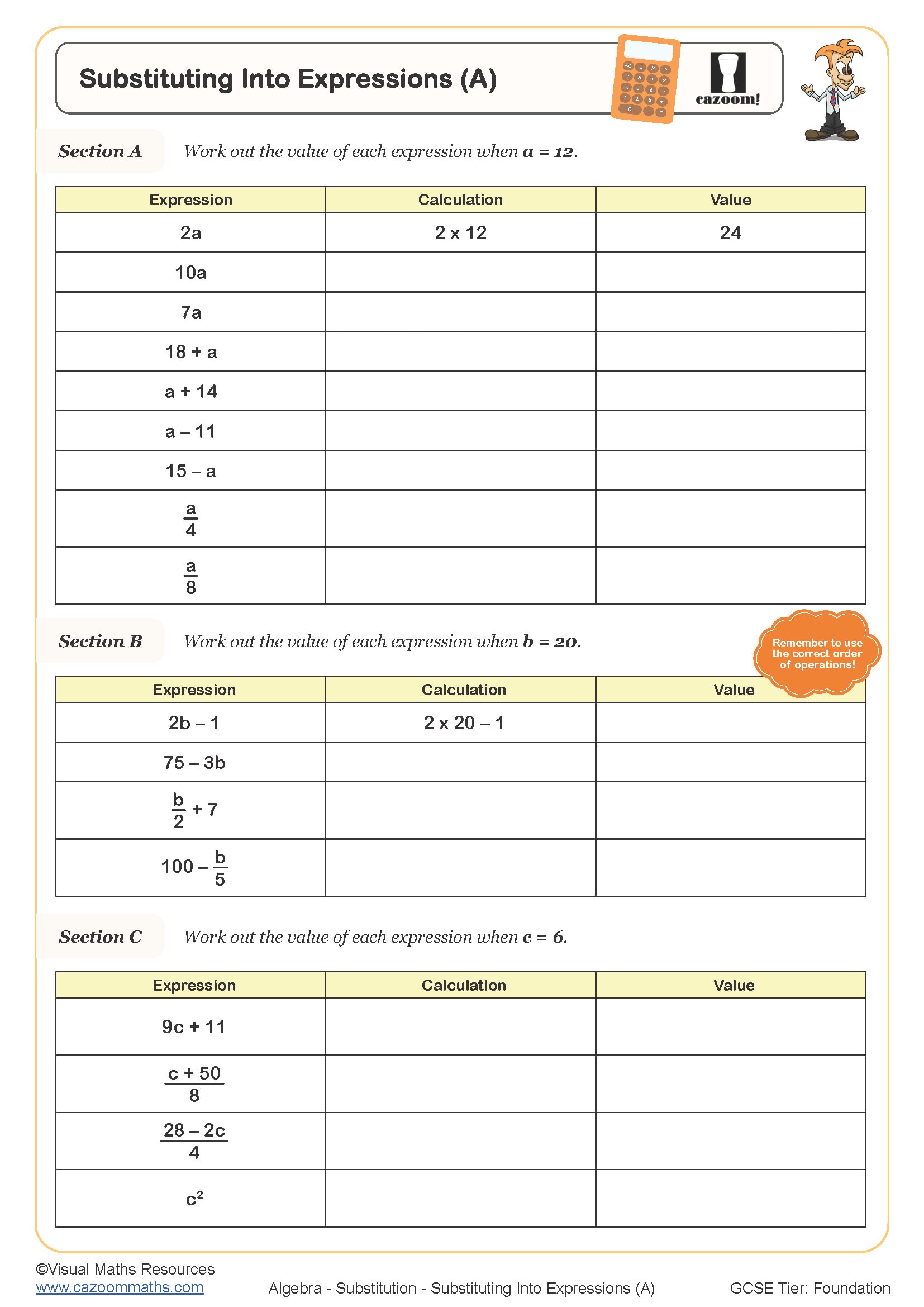
Substituting into Expressions (B)
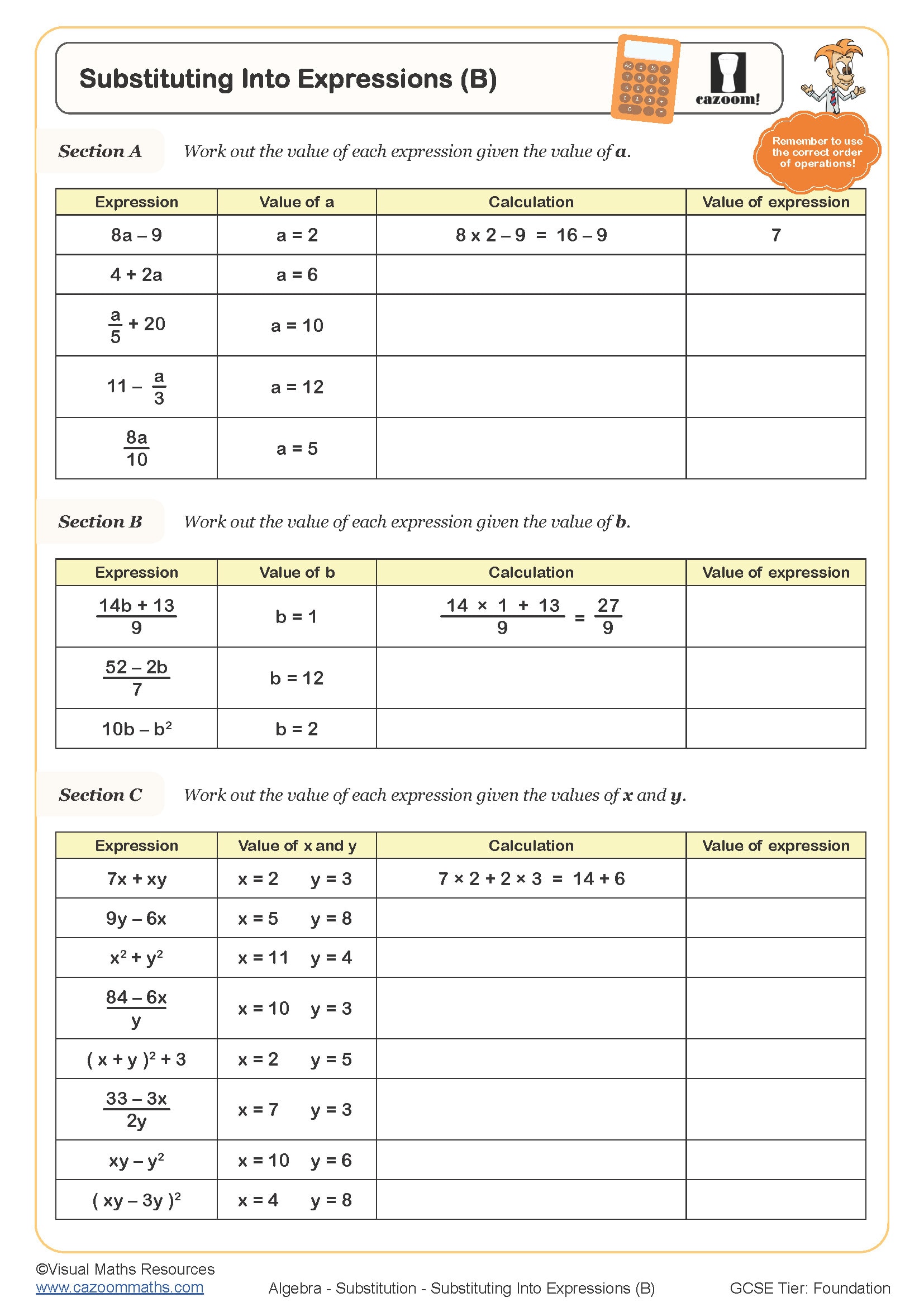
Substituting into Expressions (C)
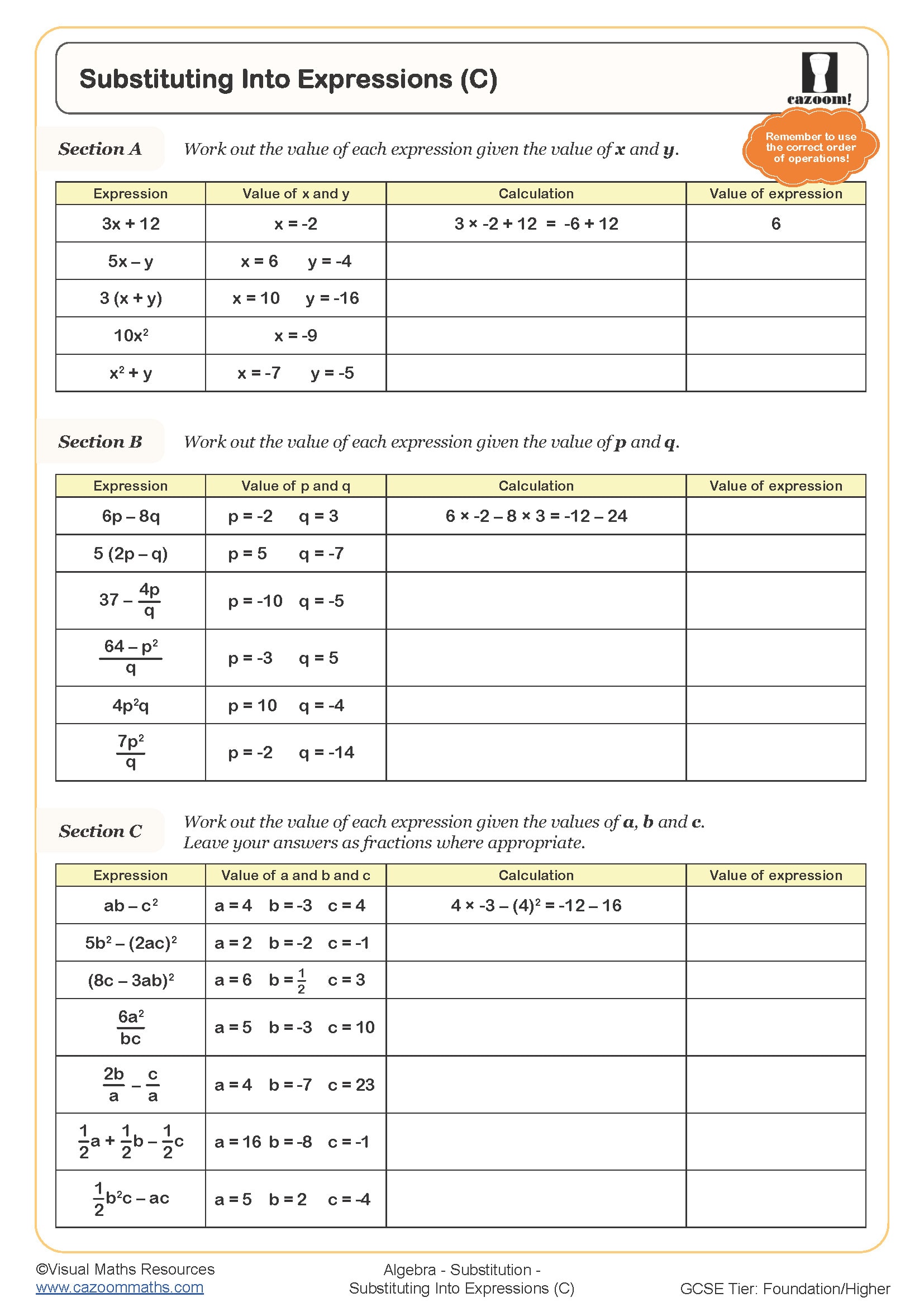
Substituting into Expressions using Negative Numbers

Substituting into Formulae (A) (With Clues)

Substituting into Formulae (A) Word Problems

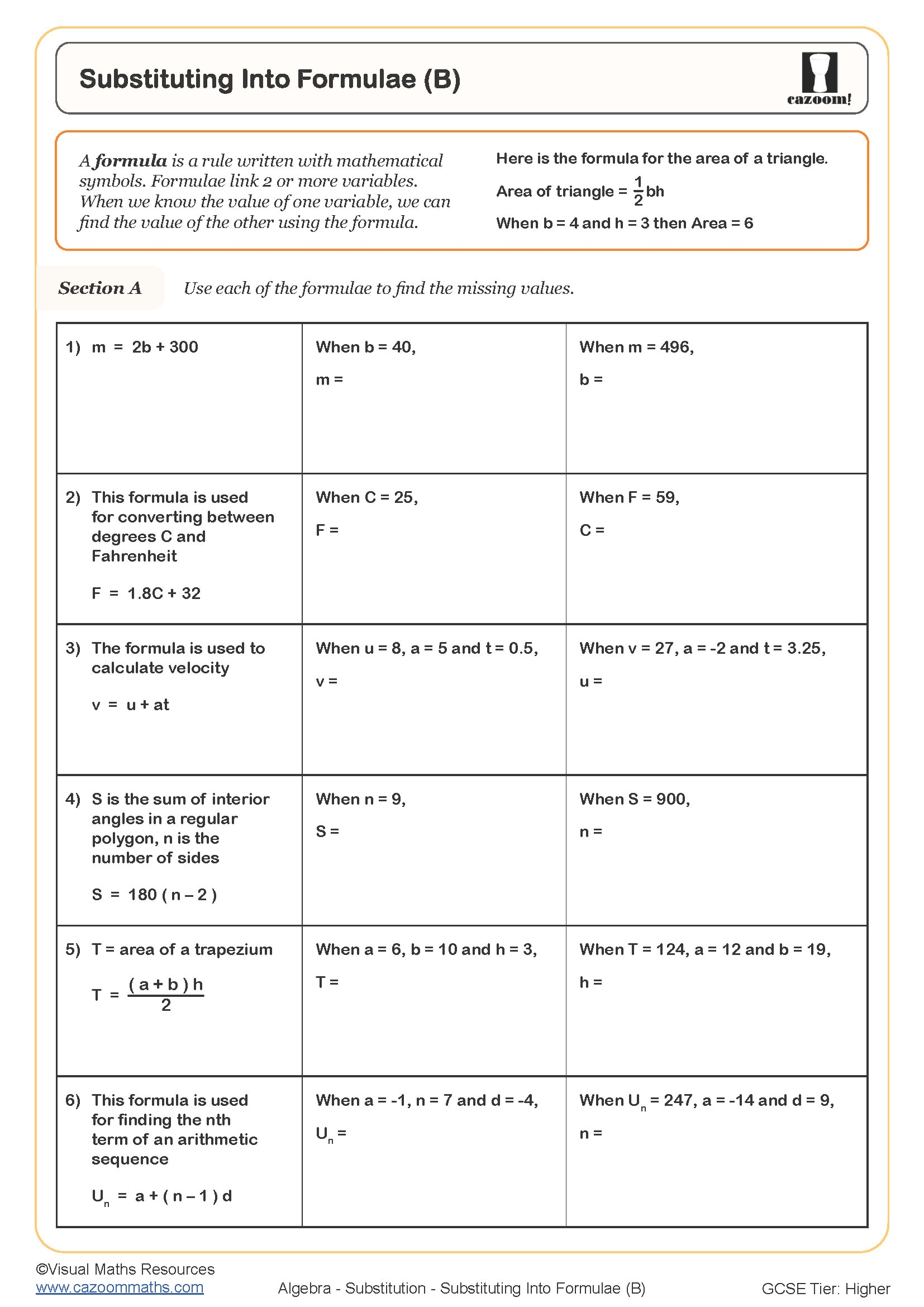
Substituting into Formulae (B)
Substituting into Quadratic Expressions
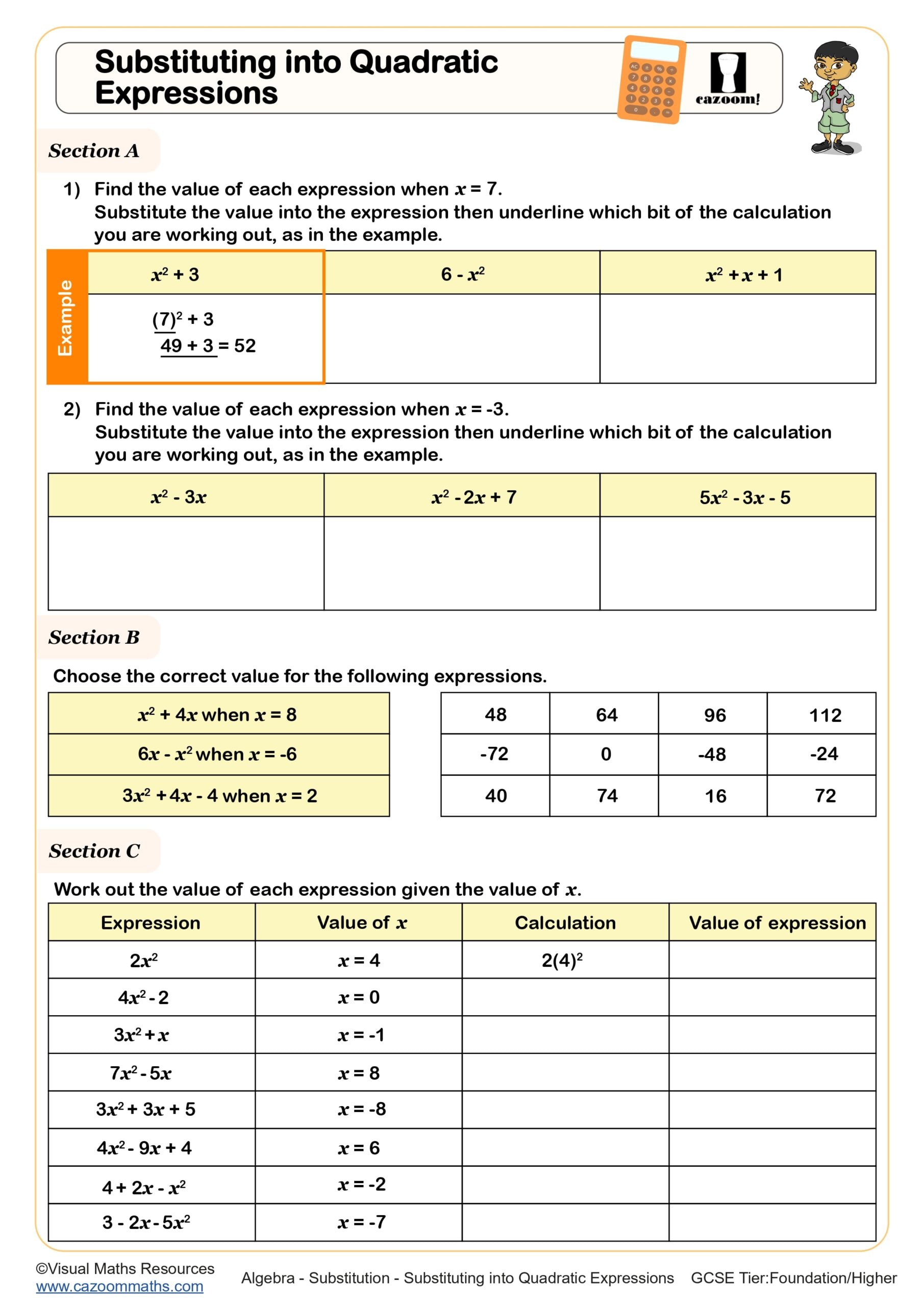
Substitution - Using Algebra Tiles
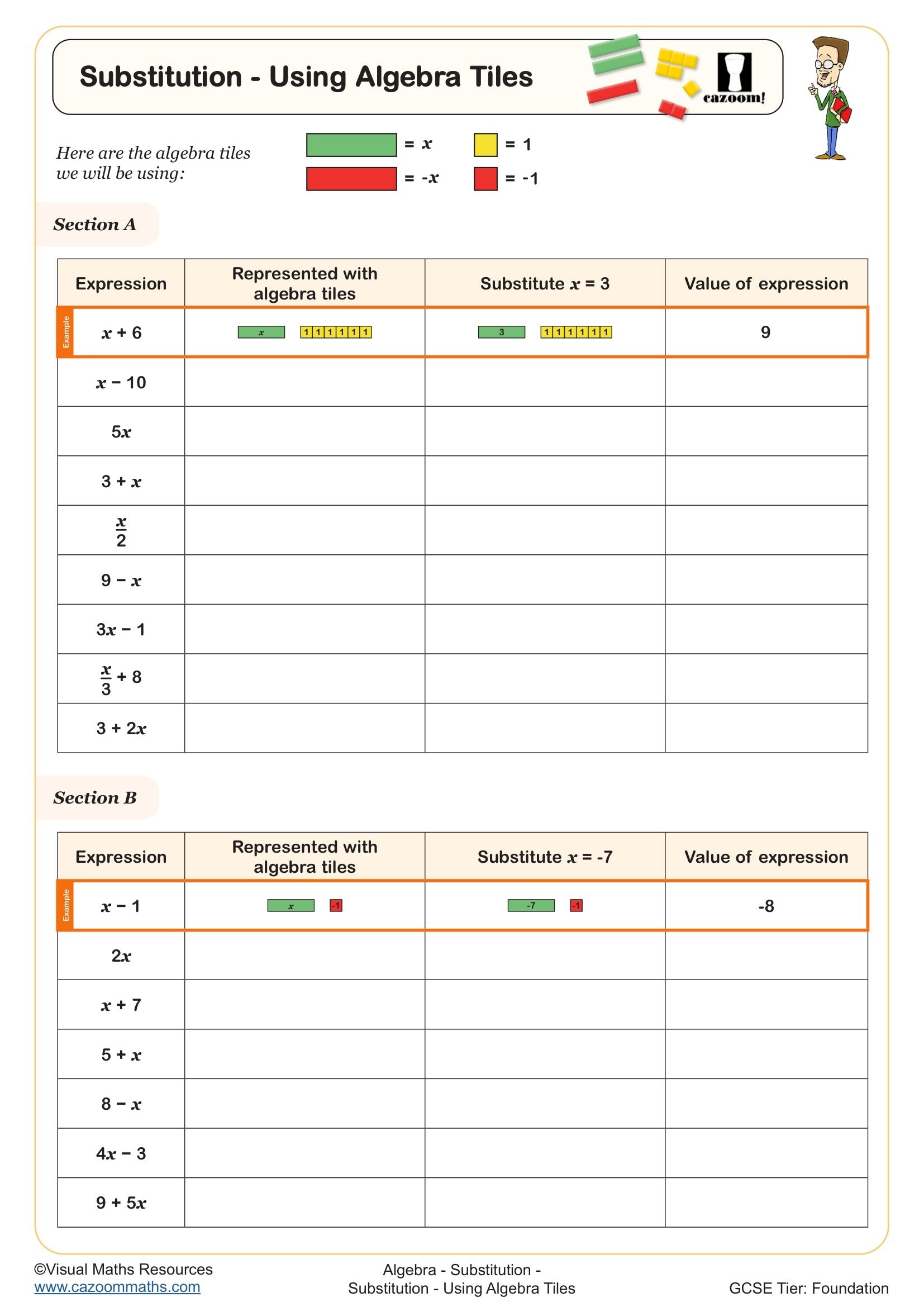
Substitution Builder (A)
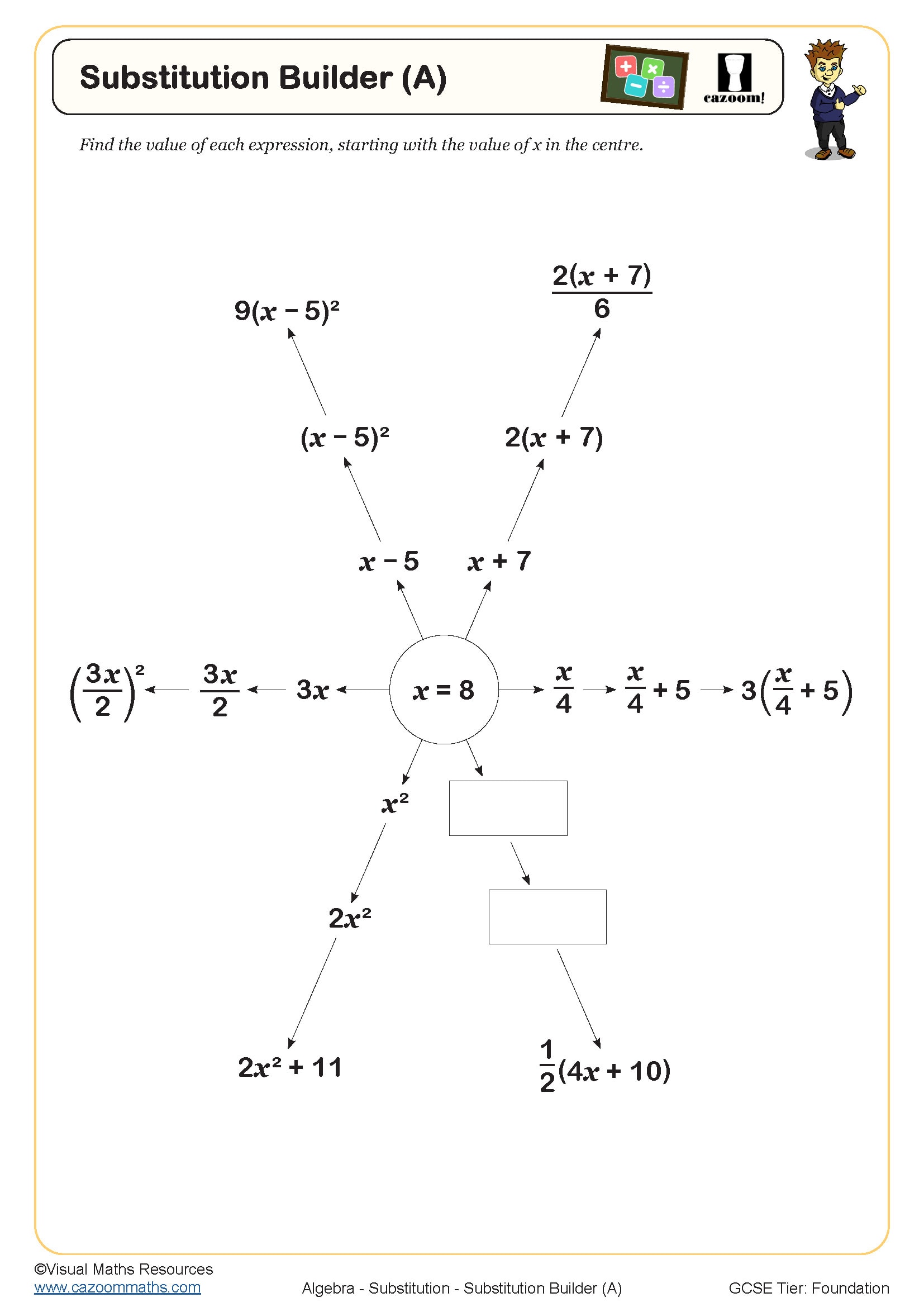
Substitution Builder (B)
Substitution Builder (C)
Substitution Magic Squares

Writing Formulae

What is substitution in maths?
Substitution in maths means replacing letters (variables) in an algebraic expression or formula with given numerical values, then calculating the result. For example, if x = 3, substituting into 2x + 5 gives 2(3) + 5 = 11. Students meet this skill early in Year 7 as part of the algebra strand in the National Curriculum, and it underpins virtually all algebraic problem-solving they'll encounter at GCSE.
Teachers often notice that students rush this process and lose marks by skipping the crucial step of showing their substitution before calculating. Writing 2(3) + 5 explicitly helps avoid errors, particularly when dealing with negative values or powers. Many students mistakenly write 2 × 3 + 5 without brackets, then calculate incorrectly when the expression involves multiple terms or indices.
Which year groups learn substitution?
These worksheets cover substitution for Year 7, Year 8, and Year 9 students across Key Stage 3. The topic first appears in Year 7 when students begin working with algebraic notation and need to understand that letters represent numbers. At this stage, expressions typically involve single variables with positive integer values, building confidence with the basic mechanics of substitution.
As students progress into Year 8 and Year 9, the complexity increases substantially. They encounter negative numbers, fractions, decimals, and expressions with multiple variables. Upper KS3 worksheets include substituting into formulae from science (such as speed, density, or area), expressions with powers and roots, and problems requiring careful attention to order of operations when brackets and indices are involved.
Why do students need to practise using substitution?
Using substitution develops students' understanding that algebra is generalised arithmetic and that letters behave according to the same mathematical rules as numbers. Regular practice helps students become fluent with the process: identify the variable, replace it with the given value, then follow order of operations to calculate accurately. This fluency is assessed directly in GCSE algebra questions and forms part of the problem-solving process in countless other contexts.
Substitution connects directly to real-world applications across STEM subjects. Engineers use substitution when checking design calculations with specific measurements, physicists substitute values into formulae to predict motion or energy, and computer programmers substitute parameters into algorithms. In finance, substitution allows professionals to calculate loan repayments or investment growth by plugging values into standard formulae, demonstrating how this apparently abstract skill underpins practical numerical reasoning.
How do these worksheets help students improve at substitution?
The worksheets build confidence through carefully structured progression, starting with straightforward expressions before introducing complications like negative numbers, brackets, and multiple variables. Many include worked examples that model the process of writing out the substitution step explicitly before calculating, which helps students develop systematic approaches that reduce careless errors. The variety of question types ensures students encounter substitution in different contexts, from pure algebraic expressions to formulae from geometry and science.
Teachers use these resources effectively for targeted intervention with students who struggle with algebraic notation, as homework to consolidate classroom teaching, or as starter activities to maintain fluency throughout the year. The complete answer sheets make them particularly useful for independent study or homework, allowing students to identify specific errors in their working. Some teachers set them as paired activities where students take turns substituting values and checking each other's calculations, which develops both accuracy and mathematical communication.