KS2 Bar Models Worksheets
Add and Subtract Fractions (A)

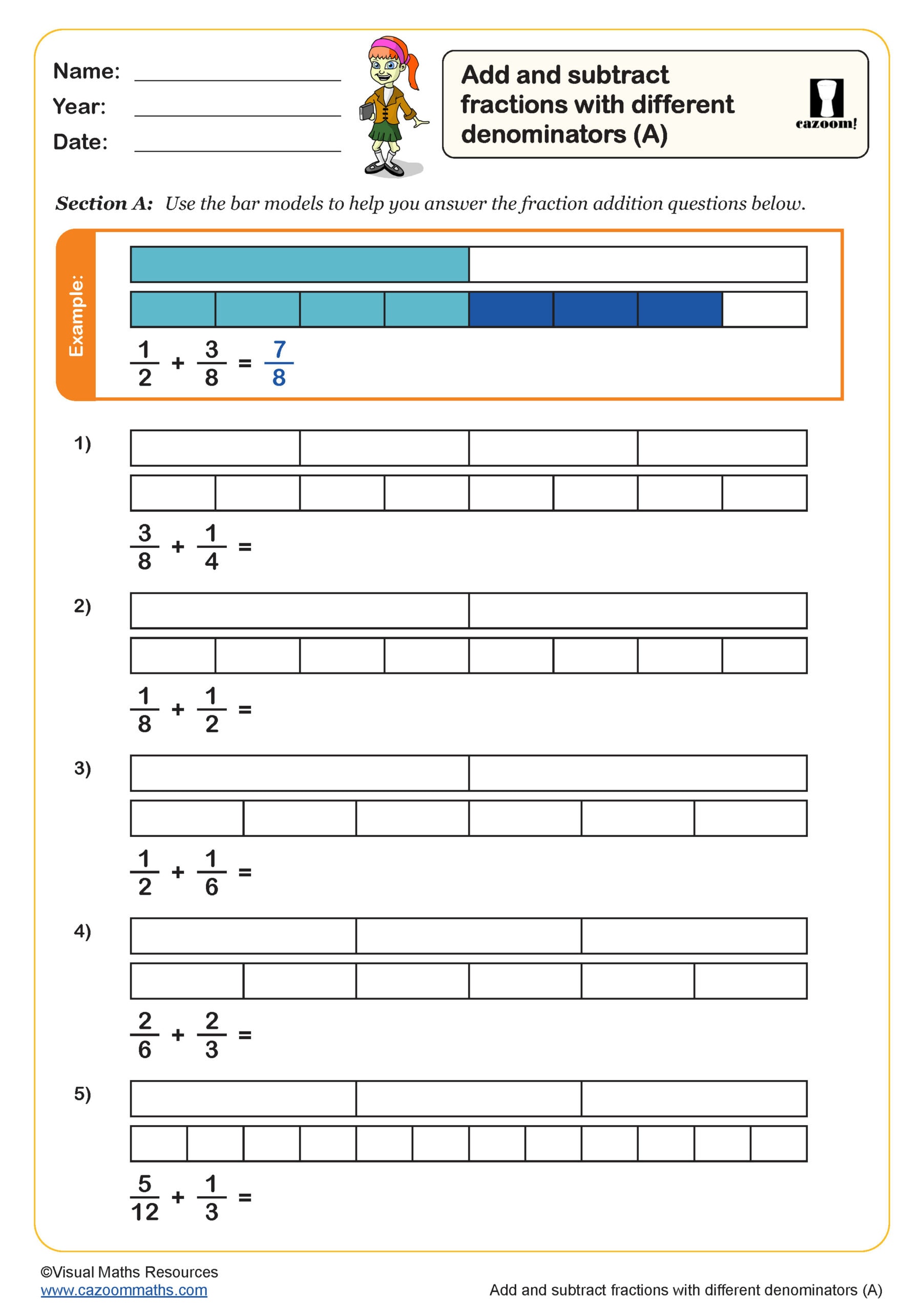
Add and Subtract Fractions with Different Denominators (A)
Angles in Triangles (A)

Compare Fractions Less Than 1

Divide Decimals by Integers (A)

Divide Decimals by Integers (B)

Equivalent Fractions Using Bar Models (A)

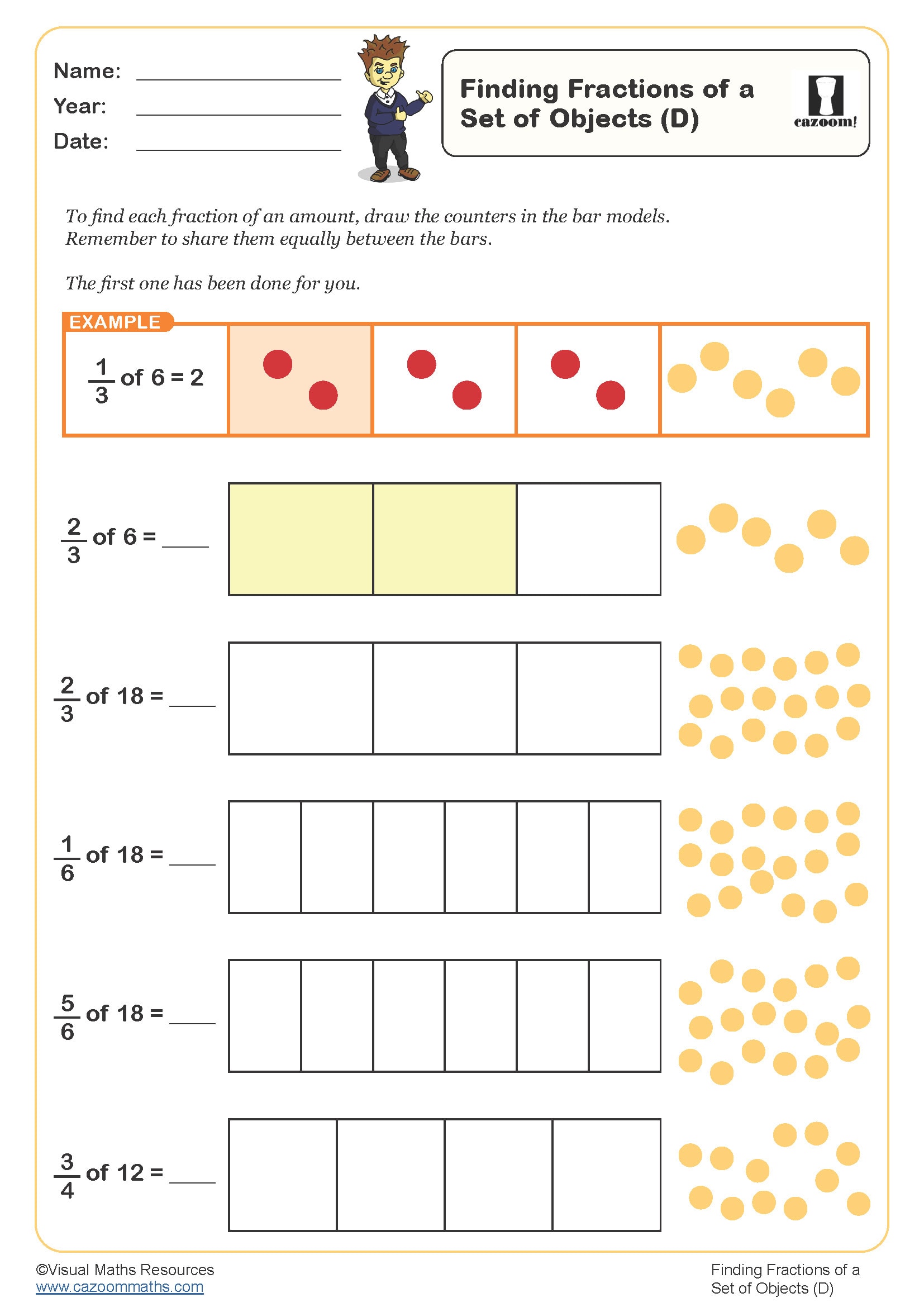
Finding fractions of a set of objects (C)
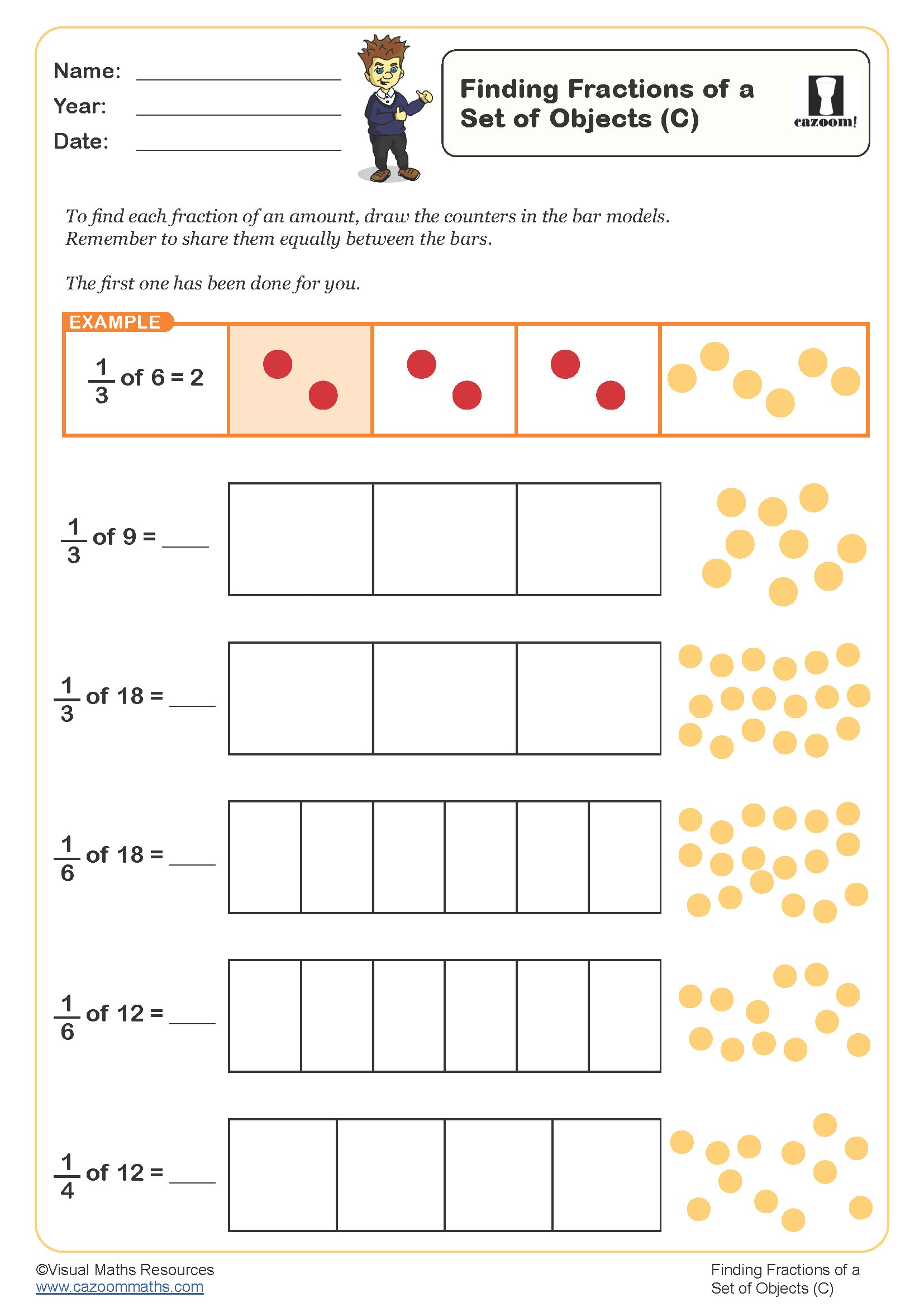
Finding fractions of a set of objects (D)
Finding Fractions of Amounts

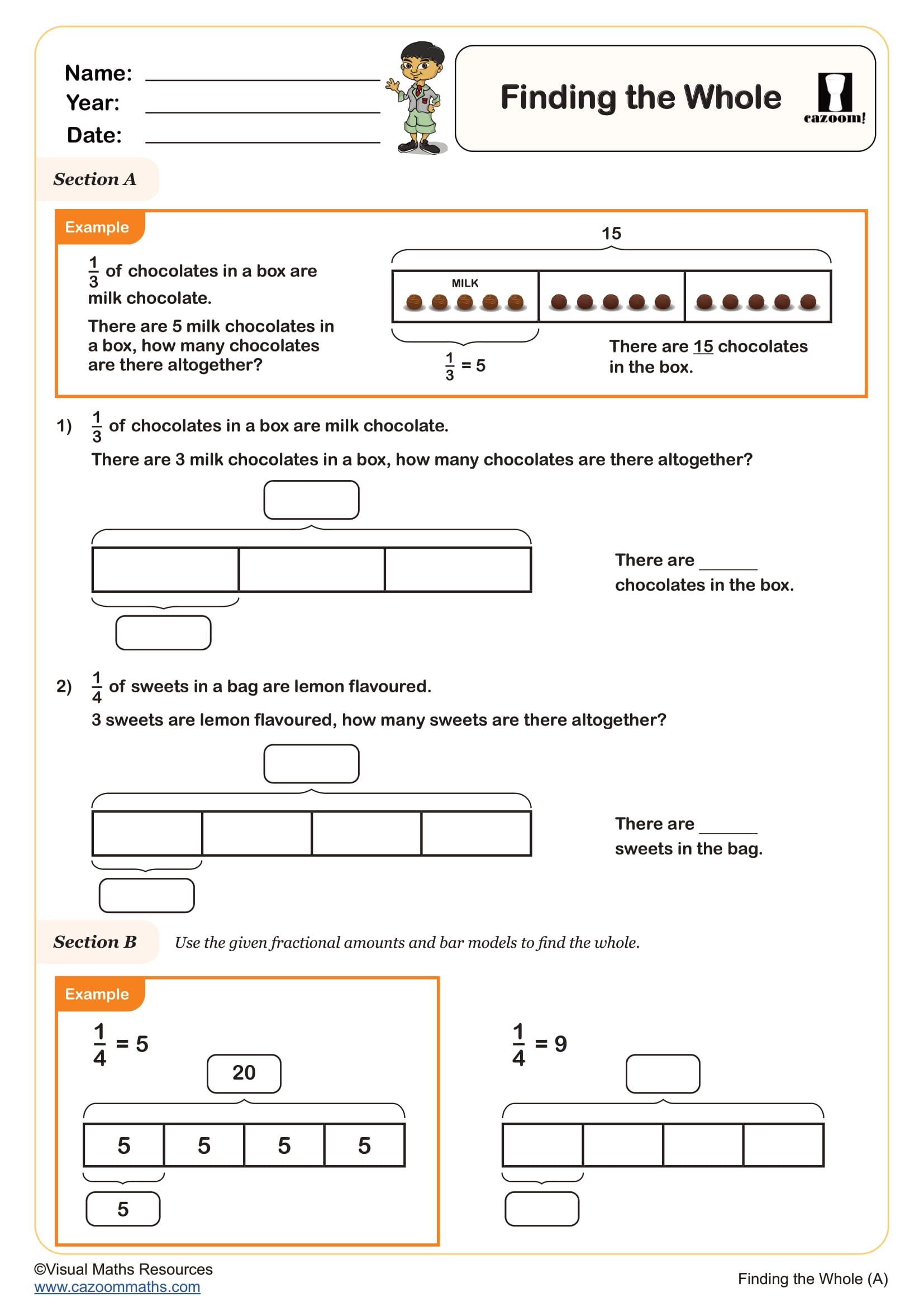
Finding the Whole
Forming One Step Equations
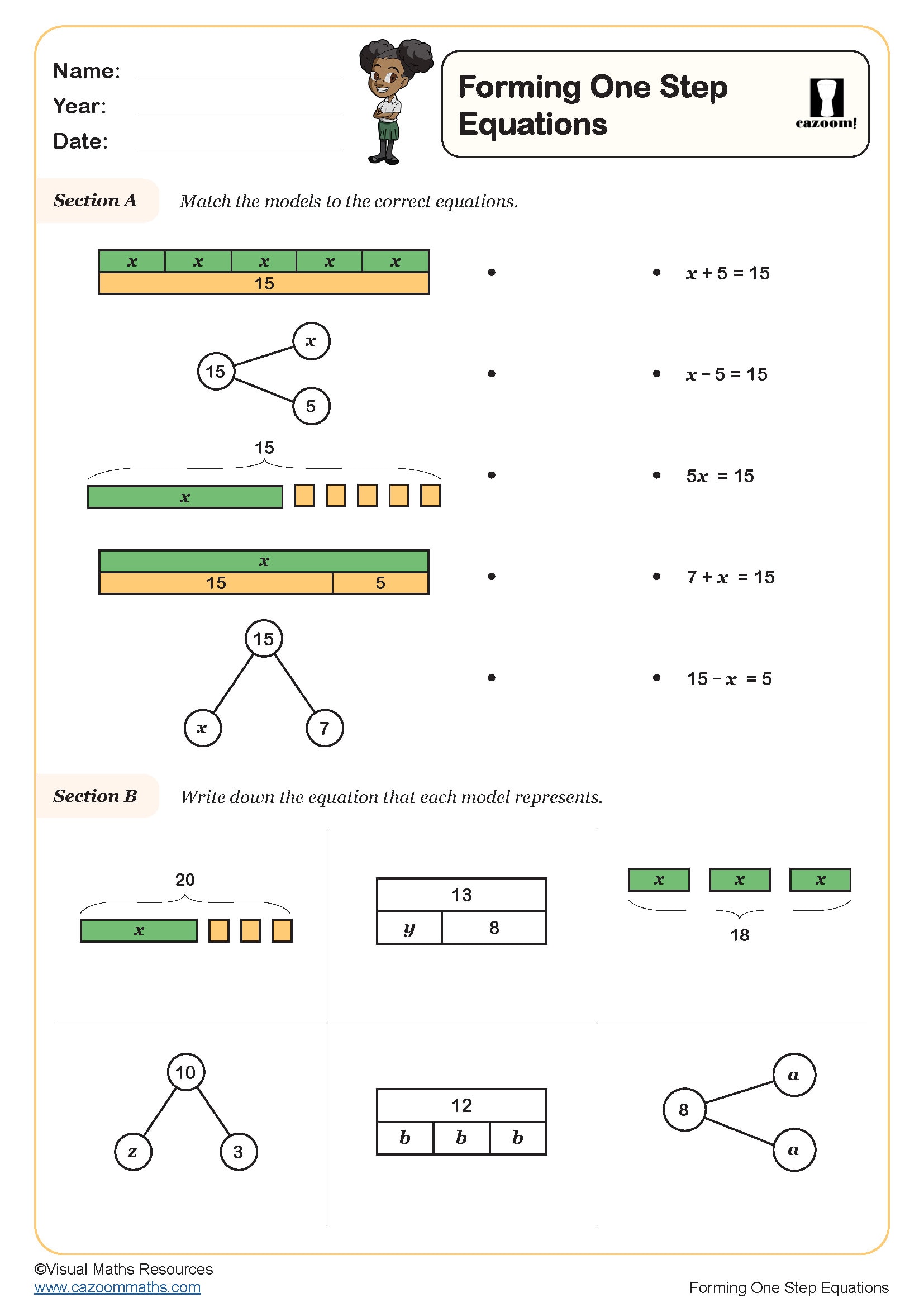
Forming One Step Equations Involving Division
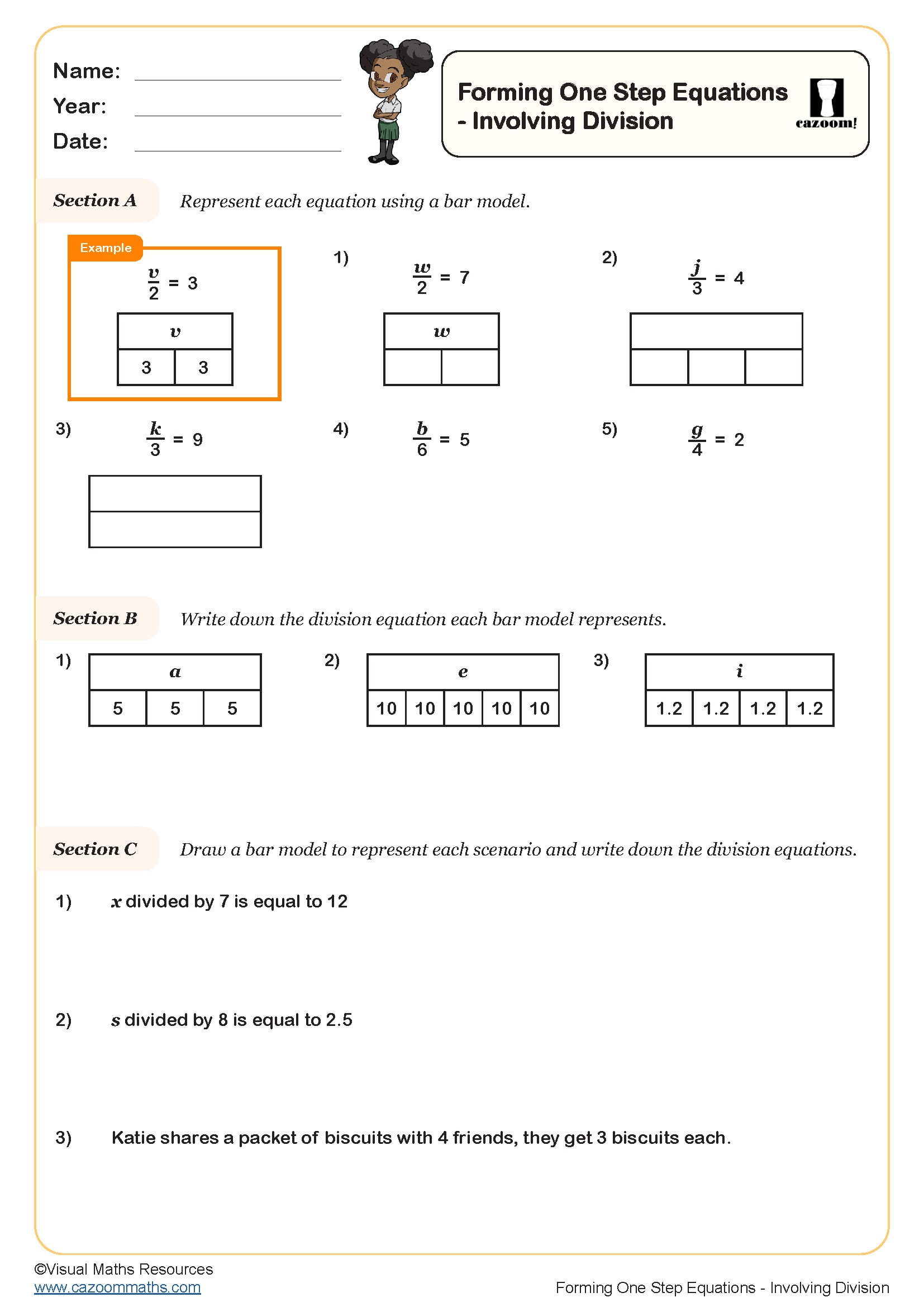
Forming Two Step Equations
Percentages of Amounts - Using a Bar Model (A)

Percentages of Amounts - Using a Bar Model (B)

Ratio - Using Bar Models (A)

Ratio - Using Bar Models (B)

Ratio and Fractions
Solving One Step Equations
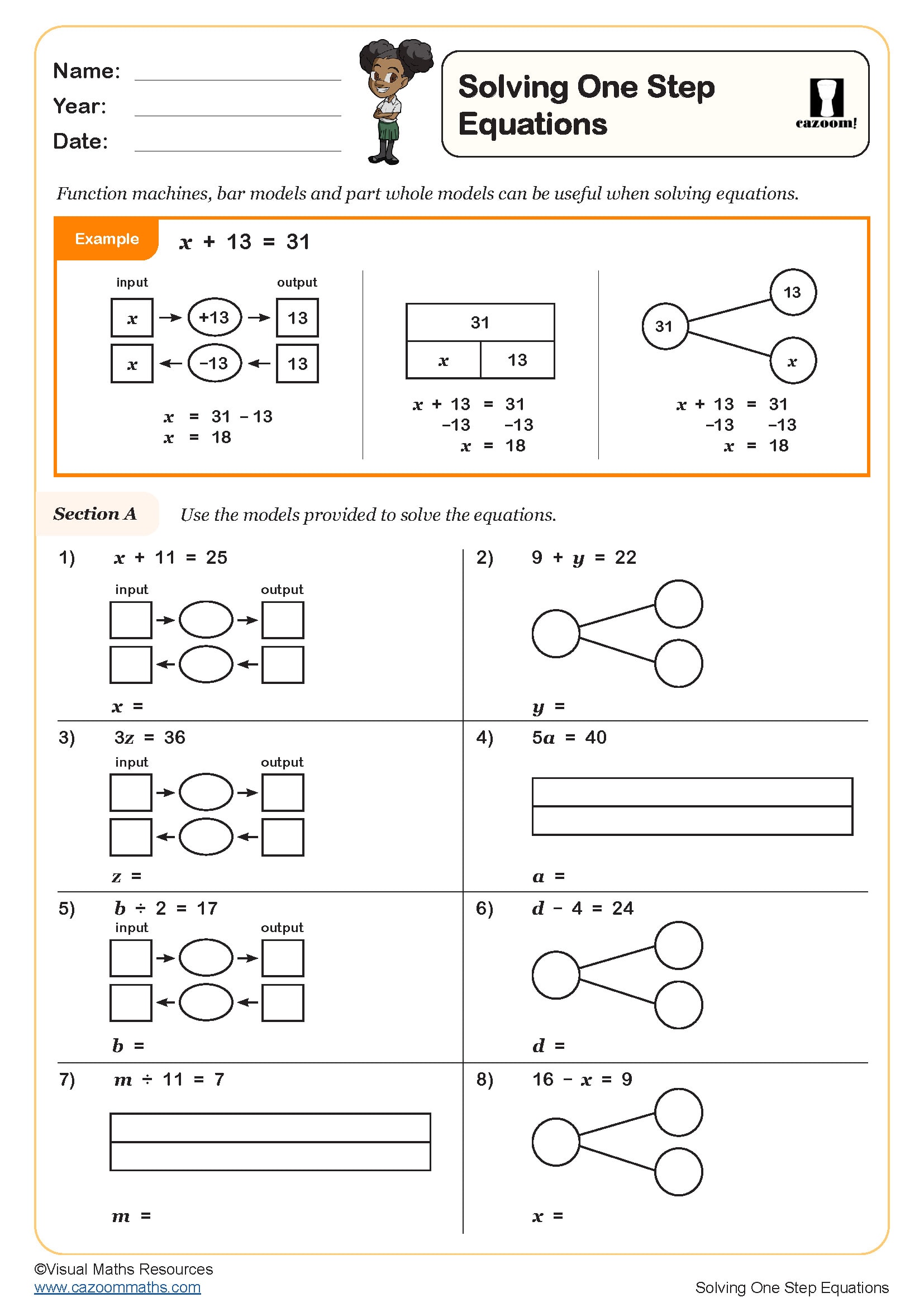
Solving Two Step Equations
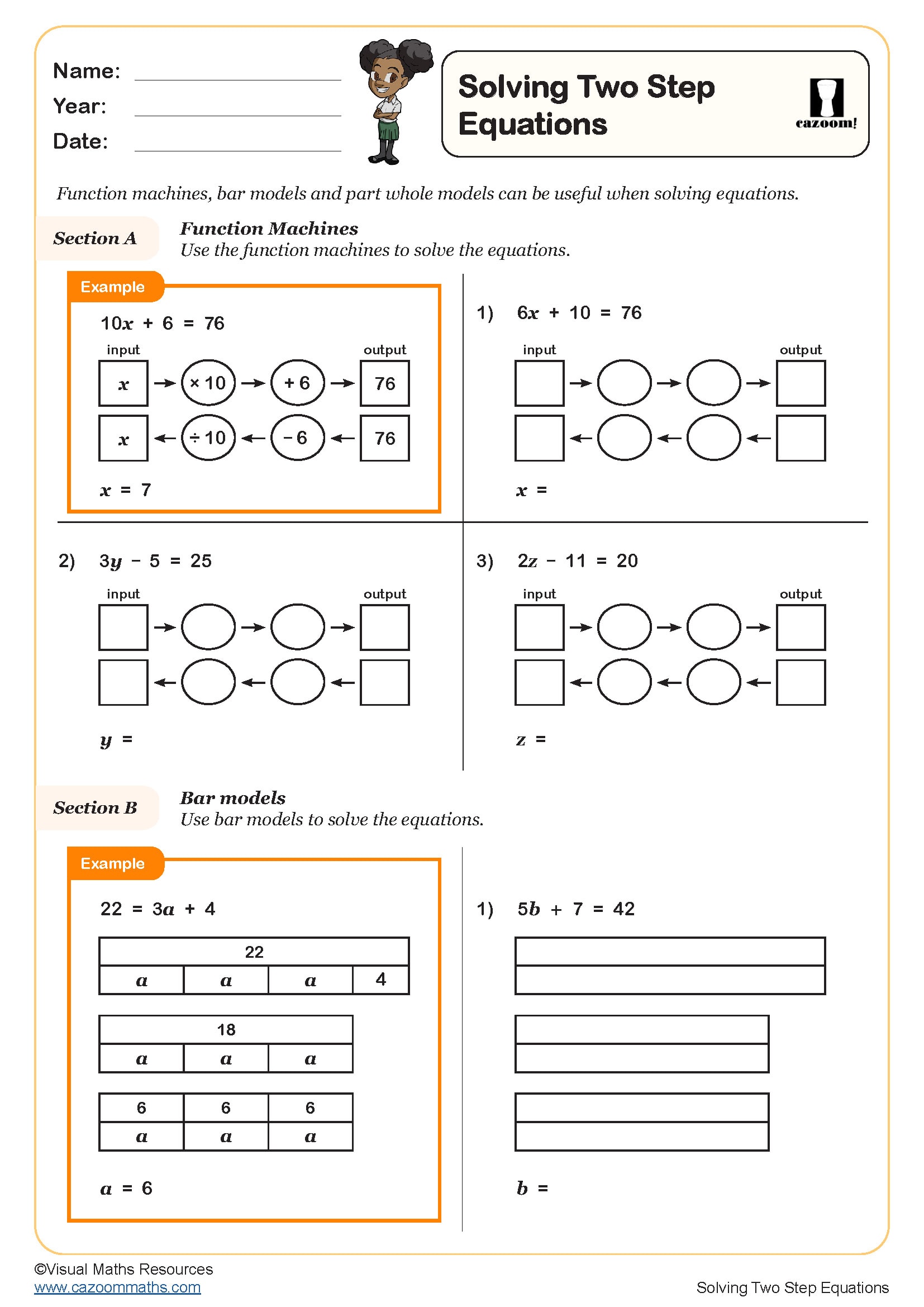
Tenths as Fractions and Decimals (A)
Tenths as Fractions and Decimals (B)

Using Inverses to Check Answers Addition and Subtraction

All worksheets are created by the team of experienced teachers at Cazoom Maths.
What Are Bar Models in KS2 Maths?
Bar models are visual representations that help pupils solve word problems by drawing rectangular bars to represent known and unknown quantities. This Singapore maths approach transforms written problems into diagrams, making the relationships between numbers clearer and more manageable. Students draw bars proportionally to show parts and wholes, enabling them to identify which operation to use.
In KS2, bar models progress from simple one-step problems to complex multi-step challenges. Early work focuses on addition, subtraction, multiplication and division, whilst later applications include fractions, decimals, percentages and ratio. The technique builds logical thinking and helps pupils tackle unfamiliar problem types with confidence, making it a cornerstone of mathematical reasoning throughout Key Stage 2.
Which Year Groups Use Bar Models?
Our bar models worksheets cover Year 3, Year 4, Year 5 and Year 6, spanning the entire KS2 curriculum. The progression ensures that skills develop systematically, with complexity increasing as pupils move through the key stage. Year 3 typically introduces the concept with straightforward comparison and part-whole problems, whilst Year 6 applies bar modelling to sophisticated ratio and proportion challenges.
Each year group builds upon prior knowledge, deepening understanding of how bar models can unlock different problem types. By Year 6, pupils use bar models confidently across fractions, percentages and algebra preparation. This structured approach ensures that students develop both the technique itself and the mathematical reasoning that makes bar modelling such a powerful problem-solving tool.
How Do Bar Models Help With Word Problems?
Bar models transform abstract word problems into visual diagrams, helping pupils identify what they know and what they need to find. Instead of guessing which operation to apply, students draw bars to represent the problem structure, making relationships between quantities explicit. This visual approach reduces cognitive load and allows pupils to focus on mathematical thinking rather than linguistic interpretation.
The method is particularly effective for comparison problems, multi-step calculations and problems involving unknown quantities. Pupils can see whether they need to combine, separate, or compare values simply by examining their diagram. This systematic approach builds problem-solving confidence and provides a reliable strategy that works across different mathematical contexts, from basic arithmetic through to more advanced proportional reasoning.
Do the Worksheets Include Answer Sheets?
Yes, every bar models worksheet includes a complete answer sheet. These answer sheets typically show the bar model diagrams alongside the numerical solutions, helping teachers mark efficiently and pupils understand both the visual representation and the calculation process. This dual presentation reinforces the connection between the model and the mathematical working.
The inclusion of answer sheets makes these resources suitable for independent practice, homework assignments, or intervention work. Pupils can check their own work and identify where their thinking diverged from the model solution. For teachers, having immediate access to worked solutions saves preparation time and ensures consistency across the class when discussing different approaches to the same problem.